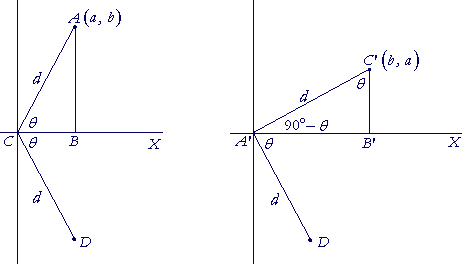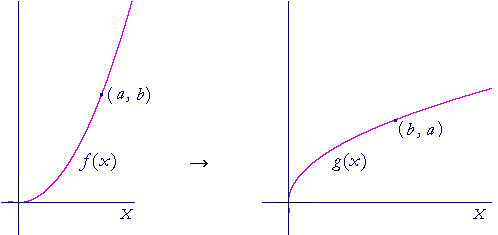19
INVERSE FUNCTIONS
The graph of an inverse function
HERE IS the definition of functions being inverses:
Functions f(x and g(x) are inverses of one another, means:
f(g(x)) = x and g(f(x)) = x,
for all values of x in their respective domains.
Why does it mean that? Because the inverse of a function undoes the action of that function. If a function g acts on a value of x, producing g(x),
then if f is the inverse, then f acting on g(x) -- f(g(x)) --will return x.
f(g(x)) = x.
And, g(f(x)) = x.
Say for example that we begin with 5, and we multiply it by 3.
3 × 5 = 15.
To undo that and return to 5, we must divide by 3.
15 ÷ 3 = 5.
Multiplication and division are inverses.
In the language of functions, let f be the function that multiplies its argument by 3. Let g be the function that divides by 3.
![]()
The function f acts on 5, producing f(5). Since g is the inverse of f, then g acting on f(5) will bring back 5.
g(f(5)) = 5.
Problem 1. Let f(x) and g(x) be inverses. Then if
f(0) = 8,
what is the value of g(8)?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
g(8) = 0.
For, f acting on 0, produces 8. Therefore, since g is the inverse, then when it acts on 8, it will bring back 0.
g(f(x)) = x.
Example 1. Addition and subtraction are inverses. Subtracting a specific number reverses, or undoes, the result of adding it.
In the language of functions, let
f(x) = x + 2, and g(x) = x − 2.
f(x) adds 2 to its argument. g(x) subtracts 2.
Upon applying the definition:
f(g(x)) = f(x − 2) = (x − 2) + 2 = x,
and
g(f(x)) = g(x + 2) = (x + 2) − 2 = x.
The definition is satisfied. The functions f and g are inverses.
Problem 2. Let f(x) = x2 and g(x) = x½. Show that they are inverses of one another. (The domain of f must be restricted to x ![]() 0.)
0.)
To show that they are inverses, we must show that they satisfy the definition of inverses.
f(g(x)) = f(x½) = (x½)2 = x,
and
g(f(x)) = g(x2) = (x2)½ = x.
When we write f(x), then x is the argument of the function.
If g is its inverse, so that
g(f(x)) = x
—then we can say that the action of g has extracted the argument x.
Example 2. Solve for x:
(x + 3)4 = 16.
Solution. To do that, we must first extract the argument, x + 3. To extract the argument of any function, simply take its inverse. In this example, take the 4th root of both sides of the equation. We can write immediately
x + 3 = 16¼.
That is,
| x + 3 | = | 2. |
| x | = | 2 − 3 = −1. |
Problem 3. Solve for x:
![]()
The inverse of taking the 5th root is taking the 5th power. Therefore, on taking the 5th power of both sides -- and thus freeing the argument:
x − 4 = 25 = 32.
x = 36.
The inverse of any function should be immediately clear. The inverse of x + 2 is x − 2. (Example 1) The inverse of x2 is x½. (Problem 2.) In Topic 21 we will see that the inverse of a logarithmic function, y = logbx, is the exponential function y = bx. And in Topic 19 of Trigonometry, we see that the inverse of y = sin x is y = arcsin x.
In calculus, the student is expected to know those inverses.
One sometimes sees that to "find" the inverse of a function, it is necessary to solve for x and exchange the variables. In fact, that is a circular method—because to apply it you must already know the inverse! If y = x2, then on exchanging sides: x = y2. To solve for y, you must know that the inverse of the square is the square root.
Compare Problem 2.
Say that we want to write the inverse of a this function:
f(x) = 3x − 4.
Suppose that x = 5. What would be the sequence of operations?
We would first multiply by 3 and then subtract 4. We would find 11. Therefore, to invert that and get back to 5, we would add 4 and then divide by 3.
| g(x) | = | x + 4 3 | . |
That function is the inverse. The student should see and understand that.
Problem 4. a) Write the inverse of f(x) = −5x.
| g(x) = | x −5 |
= − | x 5 |
Dividing by −5 is the inverse of multiplying by −5.
b) Prove that they are inverses.
| f(g(x)) = f(− | x 5 |
) = −5· | x −5 |
= x. |
And
| g(f(x)) = g(−5x) = | −5x −5 |
= x. |
f multiplies its argument by −5. g divides its argument by −5.
Problem 5. a) Let f(x) = −½x + 1. Can you immediately write its inverse, g(x)?
g(x) = −2x + 2.
For, f is the function that multiplies its argument by −½ --equivalently, divides by −2 -- and then adds 1. Its inverse will therefore first subtract 1:
x − 1
and then multiply by −2:
−2(x − 1) = −2x + 2.
b) Prove that f(x) and g(x) are inverses.
f(g(x)) = −½(−2x + 2) + 1 = x − 1 + 1 = x.
and
g(f(x)) = −2(−½x + 1) + 2 = x − 2 + 2 = x.
Problem 6. Let f(x) = 2x + 3. Write its inverse.
| g(x) | = | x − 3 2 | . |
The function I(x) = x is called the identity function. It always returns x.
As a notation for the inverse of a function f, we sometimes see f −1 ("f inverse"). "−1" is not an exponent. That notation is used because in the language of composition of functions, we can write:
f o f −1 = I
This is similar in form to the multiplication of numbers, a · a−1 = 1.
| * | * | * |
For the inverse trigonometric functions, see Topic 19 of Trigonometry.
The graph of an inverse function
The graph of the inverse of a function f(x) can be found as follows:
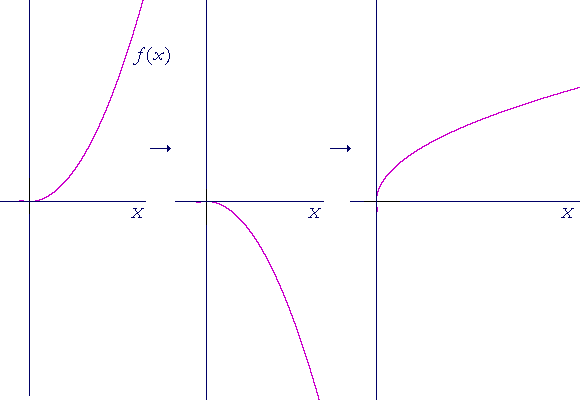
Reflect the graph about the x-axis, then rotate it 90° counterclockwise
(If we take the graph on the left to be the right-hand branch of y = x2, then the graph on the right is its inverse, y = ![]() .)
.)
To see that that is the graph of the inverse, let A be any point on
the graph of f(x), let its coördinates be (a, b), let it be a distance d from the origin C, and let AC make an angle θ with the x-axis; triangle ABC is right angled.
The figure on the left shows the reflection of A about the x-axis to the point D. The figure on the right shows the rotation of D 90° counterclockwise to the point C'.
We will see that the coördinates of C' are (b, a) -- and those are coördinates on the graph of the inverse of f (x)![]() For if we call that inverse g(x), then according to the figure on the left,
For if we call that inverse g(x), then according to the figure on the left,
f (a) = b.
And g(b) -- the figure on the right -- returns us to a:
g(b) = a.
The definition of the inverse is satisfied.
To see that the coördinates of C' are (b, a), consider that since angle C'A'D is 90°, then C'A' makes an angle of 90° − θ with the x-axis. That is, angle C'A'B' is the complement of angle B'A'D, which is angle θ. Therefore in the right triangle A'B'C', the angle at C' is equal to θ.
But the angle at A is the complement of θ. Therefore the triangles ABC, A'B'C' are congruent (Angle-side-angle), and those sides are equal that are opposite the equal angles:
A'B' is equal to AB -- which is b, the y-coördinate of f (x).
B'C' is equal to BC -- which is a, the x-coördinate of f (x).
Therefore the coördinates of C' are (b, a).
So, when each point (a, b) on f(x) is transformed into (b, a), then the graph that results is its inverse.
Each point (a, b) will also be transformed into (b, a) when (a, b) is reflected about the line y = x.
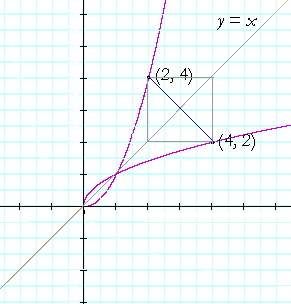
Therefore we say that the graphs of a function and its inverse are symmetrical with respect to the straight line y = x.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com