Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

CONGRUENT TRIANGLES 3
Book I. Proposition 26
WE HAVE SEEN TWO sufficient conditions for triangles to be congruent. The first, and the one on which the others logically depend, is Side-angle-side. The other is Side-side-side. We will now present the remaining condition, which is known popularly as A.S.A.: Angle-side-angle. There is no restriction, however, on which side. Therefore the theorem could also be called S.A.A.:
Side-angle-angle.
PROPOSITION 26. THEOREM
| If two triangles have two angles equal to two angles respectively, and one side equal to one side, which may be either the sides between the equal angles or the sides opposite one of them, then the remaining sides will equal the remaining sides (those that are opposite the equal angles), and the remaining angle will equal the remaining angle. |
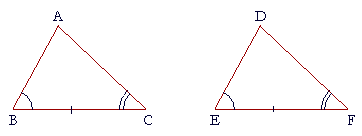
Let ABC, DEF be two triangles in which angles B and C are equal respectively to angles E and F;
let the adjoining side BC be equal to the adjoining side EF;
then AB will equal DE,
AC will equal DF,
and angle A will equal angle D.
The proof is not really difficult but it involves two cases; this one for when the adjoining sides BC, EF are equal, and another for when the sides opposite equal angles are equal: sides AB, DE; hence the proof is lengthy. Each case is proved by the indirect method, and rests ultimately on S.A.S.
Here is the case in which the sides adjoining the equal angles are equal. We want to show that the two triangles are equal in all respects.
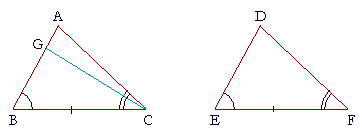
| For if AB is not equal to DE, then one of them is greater. | |
| Assume that AB is greater, and make GB equal to DE, | (I. 3) |
| and draw GC. | |
| Then since GB is equal to DE, | (Construction) |
| and BC to EF, | (Hypothesis) |
| the two sides GB, BC are equal to the two sides DE, EF respectively; | |
| and angle B is equal to angle E; | (Hypothesis) |
| therefore triangle GBC is equal to triangle DEF in all respects, and those angles are equal that are opposite the equal sides; |
(S.A.S.) |
| therefore angle GCB is equal to angle DFE. | |
| But by hypothesis, angle ACB is equal to angle DFE. | |
| Therefore angle GCB is also equal to angle ACB, the smaller to the larger, which is absurd. | |
| Therefore AB is not unequal to DE, it is equal. | |
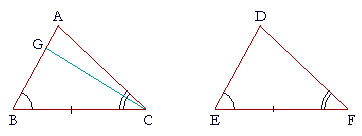 |
|
| Again, BC is equal to EF. | (Hypothesis) |
| Therefore the two sides AB, BC are equal to the two sides DE, EF respectively; | |
| and their included angles B and E are equal; | (Hypothesis) |
| therefore remaining side AC is equal to remaining side DF, and angle A is equal to angle D. | (S.A.S.) |
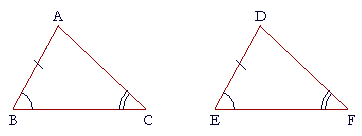
For the next case we have the same angles equal, but AB is equal to DE. We want to show that BC is equal to EF, in which case again we will have S.A.S.
The proof will be left to the student; Problem 2c.
Example 1. The straight line CD bisects the straight line AB at the point E. Angle B is equal to angle A. Prove that angle C is equal to angle D.
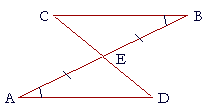
Solution. Since AB intersects CD at E,
the vertical angles BEC, AED are equal. (I. 15)
And we are given that angle A is equal to angle B,
and that side AE is equal to side EB,
which are the sides between the equal angles.
Therefore the remaining angle is equal to the remaining angle:
angle C is equal to angle D. (A.S.A.)
Which is what we wanted to prove.
Example 2. AB and CD are straight lines that intersect at E;
CE is equal
to EB, and angle CFA is equal to angle BGD.
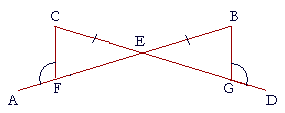
Prove that CF is equal to BG.
Solution. Since angle CFA is equal to angle BGD,
then angle CFE is equal to angle BGE,
because they are supplements of equal angles. (I. 13, Problem 6.)
And angle FEC is equal to angle GEB,
because they are vertical angles.
Therefore angles CFE, FEC are equal to angles BGE, GEB respectively;
and side CE is equal to side BE; (Hypothesis)
therefore triangles CEF, BEG are congruent, (S.A.A.)
and therefore CF is equal to BG.
Which is what we wanted to prove.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com