12
IRRATIONAL NUMBERS
The relationship of arithmetic to geometry
The invention of irrational numbers
THE JOB OF ARITHMETIC when confronted with geometry, that is, with things that are continuous -- length, area, time -- is to come up with the name of a number to be its measure. For if we say that a length is 3½ meters,

then the number "3½" names the ratio of that length to 1 meter. (Lesson 7.) With a different unit of measure -- 1 inch, 1 foot, 1 mile -- the "length" of that line would be a completely different number.
But is there a number to name every ratio to a unit? If the square
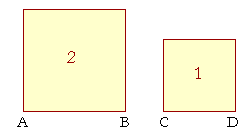
on AB is to the square on CD in the ratio 2 : 1, then AB, CD themselves are incommensurable, and no rational number can name their ratio. For, any two rational numbers always have a common measure.
Incommensurability has been and is the logical sticking point in the relationship of arithmetic to geometry. It is not only an intellectual problem, but it has been an extremely practical one in the history of mathematics. For if we want to involve AB, CD in some calculation, what number would we write? AB = ? × CD.
The invention of irrational numbers

We have seen that when two squares are in the same ratio as two square numbers, then their sides will have the same ratio as the square roots. Nevertheless, if CD were 1 meter, then we would like to say that AB is "Square root of 2" meters -- but there is no such rational number. For if there were, then again, AB, CD would have a common measure, which they do not.
If we insist, however, that there be a number to indicate the ratio of AB to CD, then we keep the name "Square root of 2," and we call it an irrational number. Its numeral is ![]() . That is,
. That is,
![]() ×
× ![]() = 2.
= 2.
![]() is that number which when multiplied by itself -- when squared -- is 2. "Square root of 2" is its name. It is not any whole number, any fraction, any mixed number or any decimal -- it is not any rational number. It is a pure creation.
is that number which when multiplied by itself -- when squared -- is 2. "Square root of 2" is its name. It is not any whole number, any fraction, any mixed number or any decimal -- it is not any rational number. It is a pure creation.
| Now, | 7 5 |
is close to |
| 7 5 |
× | 7 5 |
= | 49 25 |
-- which is almost 2. But to prove that there is no rational number whose square is 2, suppose there were. Then we could express it as a fraction ![]() in lowest terms. That is, suppose
in lowest terms. That is, suppose
| m n |
× | m n |
= | m × m n × n |
= 2. |
But that is impossible. Since ![]() is in lowest terms, then m and n have no common divisors except 1. Therefore, m × m and n × n also have no common divisors. It will be impossible to divide n × n into m × m and get 2.
is in lowest terms, then m and n have no common divisors except 1. Therefore, m × m and n × n also have no common divisors. It will be impossible to divide n × n into m × m and get 2.
There is no number of arithmetic -- no rational number -- whose square is 2.
Naturally we wonder, "How much is ![]() ?" We can only answer approximately. As a fraction, we saw it is almost
?" We can only answer approximately. As a fraction, we saw it is almost ![]() . As a decimal, it is approximately 1.414. How would anyone know that? Again, because 1.414 squared is almost 2.
. As a decimal, it is approximately 1.414. How would anyone know that? Again, because 1.414 squared is almost 2.
1.414 × 1.414 = 1.999396.
We could come closer to ![]() by approximating it with more decimal digits. But no decimal squared will ever be
exactly 2.
by approximating it with more decimal digits. But no decimal squared will ever be
exactly 2. ![]() is irrational.
is irrational.
It was argued for many centuries whether ![]() "really" is a number. Mathematicians thought of
"really" is a number. Mathematicians thought of ![]() as a convenient symbol with which to calculate, but as for its being a number, that was something else. For, every rational number can be constructed from 1, which is the source. A whole number is a number of 1's. A fraction is a number of unit fractions. But an irrational number is not a number of anything. That is the great problem of the irrational.
as a convenient symbol with which to calculate, but as for its being a number, that was something else. For, every rational number can be constructed from 1, which is the source. A whole number is a number of 1's. A fraction is a number of unit fractions. But an irrational number is not a number of anything. That is the great problem of the irrational.
In the next Lesson, we will investigate in what sense irrational numbers exist. And we will return to our original inquiry:
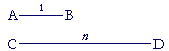
If AB, CD are lengths, will there always be a number n -- rational or irrational -- such that, proportionally,
AB is to CD as 1 is to n?
In any event, ![]() is not the only irrational number. Let us illustrate that by asking:
is not the only irrational number. Let us illustrate that by asking:
The square roots of which natural numbers are rational?
Answer. Only the square roots of square numbers.
![]() = 1 is rational.
= 1 is rational.
![]() ,
, ![]() are irrational.
are irrational.
![]() = 2 is rational.
= 2 is rational.
![]() ,
, ![]() ,
, ![]() ,
, ![]() are irrational.
are irrational.
![]() = 3 is rational.
= 3 is rational.
And so on.
Problem 1. Say the name of each number.
| a) |
Square root of 3. | b) |
Square root of 5. | |
| c) |
Two. It's rational. | d) |
Square root of 3/5. | |
| e) |
Three-fifths. | f) |
One. | |
Problem 2. Which of the following are rational numbers and which are irrational?
| a) |
Irrational. | b) |
Rational. | |
| c) |
Rational. | d) |
Irrational. | |
A common measure with 1
We have seen that every rational number has the same ratio to 1 as two natural numbers. We can always say, then, how a rational number is related to 1. Every rational number and 1 will have a common measure. An irrational number, then, is a number that has no common measure with 1. It will not be possible to say how an irrational number and 1 are related.
![]() and 1 are incommensurable.
and 1 are incommensurable.
Problem 3. What number is a common measure of each pair?
a) 1 and 5 1
| b) 1 and | 5 8 |
1 8 |
c) 1 and 2.617 .001
d) 1 and ![]() None.
None.
Problem 4. Why were irrational numbers invented?
To have a name for the relationship of incommensurable magnitudes. In algebra, it was so that the solution of any quadratic equation—e.g. x2 = 2—would have a name.
Problem 5. The squares on the sides of triangle ABC are in the ratio 1 : 4 : 3. Express the ratio of each pair of sides as a ratio of numbers, whether rational or irrational.
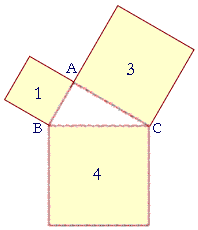
a) AB : BC =
1 :
2
b) BC : CA =
2 :
![]()
c) CA : AB =
![]() :
1
:
1
| d) | |
5 7 |
, or | 12 7 |
. |
| How could you know that? | |||||
| 12 7 |
· | 12 7 |
= | 144 49 |
-- which is almost 3. |
| e) | Use that approximation to approximate the ratio of BC to CA as a ratio of natural numbers. |
| BC : CA = 2 : | 12 7 |
= 14 : 12 = 7 : 6 |
Problem 6. One square is four fifths of another.
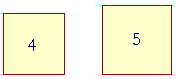
a) Are the sides commensurable?
No. 4 and 5 are not both square numbers.
b) Express the ratio of the sides as a ratio of numbers.
2 : ![]()
c) Are the squares commensurable?
Yes. They are in the same ratio as natural numbers.
Next Topic: The existence of irrational numbers
Copyright © 2020 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
