a) 1 : 2 = 5 : 10	b) 3 : 9 = 10 : 30	c) 4 : 1 = 20 : 5

d) 49 : 7 = 56 : 8	e) 6 : 42 = 9 : 63	f) 18 : 2 = 45 : 5

g) 2 : 3 = 10 : 15	h) 3 : 4 = 75 : 100	i) 2 : 5 = 20 : 50

Problem 3.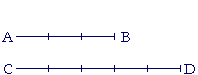

AB, CD are straight lines, and AB is three fifths of CD. Express that ratio as a proportion.

Example 1. If, proportionally, a : b = 3 : 4, then, explicitly, what ratio has a to b?

Answer. The proportion implies the ratio of a to b, but it does not state that ratio explicitly. What ratio has 3 to 4? 3 is three fourths of 4. Explicitly, then, that is the ratio of a to b. a is three fourths of b.

Proportions imply ratios.

Problem 4. Explicitly, what ratio has x to y?

a) x : y = 1 : 5. x is the fifth part of y.

b) x : y = 32 : 8. x is four times y.

c) x : y = 7 : 10. x is seven tenths of y.

The theorem of the alternate proportion

The numbers in a proportion are called the terms: the 1st, the 2nd, the 3rd, and the 4th.

1st : 2nd = 3rd : 4th

We say that the 1st and the 3rd are corresponding terms, as are the 2nd and the 4th.

The following is the theorem of the alternate proportion:

If four numbers are proportional, then the
corresponding terms are also proportional.

As the first term is to the third, so the second will be to the fourth.

a : b = m : n,

then, alternately,

a : m = b : n.

(Euclid, VII. 13.)

For example, since

1 : 3 = 5 : 15,

then alternately,

1 : 5 = 3 : 15.

(Skill in Arithmetic: Lesson 17, Question 2.)

Problem 5. State the alternate proportion.

a)	10 : 30 = 5 : 15	b)	2 : 8 = 6 : 24

	10 is to 5 as 30 is to 15.		2 is to 6 as 8 is to 24.

c)	2 : 3 = 10 : 15

	2 is to 10 as 3 is to 15.

This leads to:

The theorem of the same multiple

Let us complete this proportion,

4 : 5 = 12 : ?

4 is four fifths of 5 (Lesson 2), but it is not obvious of what number 12 is four fifths.

Alternately, however, 4 is the third part of 12 -- or we could say that 4 has been multiplied by 3. Therefore, 5 also must be multiplied by 3 --

4 : 5 = 12 : 15

That is,

4 : 5 = 3 × 4 : 3 × 5.

This is called the theorem of the same multiple.

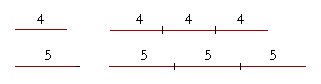
Three 4's; three 5's

4 is four fifths of 5. But each 4 has that same ratio to each 5. Two 4's, then, upon adding them, will have that same ratio to two 5's. Three 4's will have that same ratio to three 5's. And so on. Any number of 4's will have that same ratio, four fifths, to an equal number of 5's.

Here is how we state the theorem:

If we multiply two numbers by the same number,
then the products will have the same ratio
as the numbers we multiplied.

(Euclid, VII. 17.)

Problem 6. Write five pairs of numbers that have the same ratio as 3 : 4.

Problem 7. Complete each proportion.

a) 4 : 9 = 8 : 18	b) 4 : 9 = 12 : 27	c) 4 : 9 = 16 : 36

d) 7 : 8 = 21 : 24	e) 9 : 5 = 63 : 35	f) 4 : 11 = 20 : 55

g) 2 : 9 = 16 : 72	h) 6 : 5 = 54 : 45	i) 8 : 3 = 56 : 21

Problem 9. Complete this proportion, 2.45 : 7 = 245 : 700.

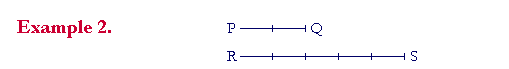
PQ is two fifths of RS. If PQ is 12 miles, then how long is RS?

Solution. Since PQ is two fifths of RS, then proportionally,

PQ : RS = 2 : 5.

If PQ is 12 miles, then

PQ : RS = 2 : 5 = 12 miles : ? miles.

That is, 12 miles corresponds to PQ and 2. And since 12 is 6 × 2, the missing term is 6 × 5:

PQ : RS = 2 : 5 = 12 miles : 30 miles.

RS is 30 miles.

Or, since

PQ : RS = 2 : 5,

then inversely,

RS : PQ = 5 : 2.

Now, what ratio has 5 to 2? 5 is two and a half times 2. RS therefore is two and a half times PQ. And if PQ is 12 miles, then RS is 24 + 6 = 30 miles.

Problem 10.

AB is three fourths of CD. Specifically, AB is 24 cm. How long is CD?

The theorem of the common divisor

Since we may multiply both terms by the same number, then, symmetrically, we may divide both terms by the same number.

25 : 40 = 5 : 8

upon dividing both 25 and 40 by 5.

Explicitly, then, we see that 25 is five eighths of 40.

Problem 11. Explicitly, what ratio has 16 to 40? Express that ratio so that the terms have no common divisors (except 1).

Lowest terms

When the terms of a ratio have no common divisors except 1, then we have expressed their ratio with the lowest terms. They are the smallest terms -- the smallest pair of numbers -- that have that ratio.

Problem 12. Explicitly, what ratio have the following? Express each ratio with the lowest terms.

a) 6 is three fourths of 8, upon dividing each term by 2.

b) 12 is two thirds of 18.		c) 10 is two fifths of 25.

d) 9 is three eighths of 24.		e) 6 is three fifths of 10.

f) 90 is nine tenths of 100.		g) 72 is eight ninths of 81.

h) 16 is four fifths of 20.		i) 21 is three tenths of 70.

The theorem of extremes and means

If four numbers are proportional,

a : b = c : d,

then the product of the extremes is equal to the product of the means.

ad = bc.

And conversely.

For, if

a : b	=	c : d,

then on multiplying both a and b by d, and c and d by b,

ad : bd	=	bc : bd.

Therefore alternately,

ad : bc	=	bd : bd.

But bd is equal to bd. Therefore,

ad	=	bc.

Which is what we wanted to prove.

By working the proof backwards, we could show that, conversely, if

ad	=	bc,
then
a : b	=	c : d.

This theorem, or at any rate its algebraic version, seems to be the only one taught in the schools, and it has become the mechanical method for solving all ratio problems. The student should resist that tempatation and should understand the facts of ratio and proportion. We include it here only for the purpose of explaining the following:

Example 3. If a and b are numbers such that four a's are equal to three b's,

Four a's are equal to three b's,

then what ratio has a to b?

Answer. Three fourths. For since

4a	=	3b,
then according to the theorem of extremes and means,
a : b	=	3 : 4.

a is three fourths of b.

Problem 13. If eight m's are equal to five n's, then what ratio has

m to n?

The language of ratio

Example 4. Joan earns $1600 a month, and pays $400 for rent. Express that fact in the language of ratio.

Answer. "A quarter of Joan's salary goes for rent."

That sentence, or one like it, expresses the ratio of $400 to $1600, of the part that goes for rent to her whole income. We are not concerned with the numbers themselves, but only their ratio.

Example 5. In Erik's class there are 30 pupils, while in Ana's there are only 10. Express that fact in the language of ratio.

Answer. "In Erik's class there are three times as many pupils as in Ana's."

This expresses the ratio of 30 pupils to 10.

Example 6. In a class of 24 students there were 16 B's. Express that fact in the language of ratio.

Answer. "Two thirds of the class got B."

This expresses the ratio of the part that got B to the whole number of students; 16 out of 24. Their common divisor is 8. 8 goes into 16 two times and into 24 three times. 16 is two thirds of 24.

Problem 14. Express each of the following in the language of ratio. Use a complete sentence.

a) In a class of 30 pupils, there were 10 A's.

b) Out of 120 people surveyed, 20 responded No.

c) The population of Eastville is 60,000, while the population of
d) Westville is 20,000.

d) Over the summer, John saved $1000, while Bob has saved only $100.

e) At a party, there were 12 girls and 4 boys.

f) In a class of 28 students, there were 21 A's.

g) In a survey of 60 people, 40 answered Yes.

h) In a class of 40 pupils, 25 got a B.

i) Of the 2100 students who voted, 1400 voted for Harrison.

j) This month's bill is $50, while last month's was only $20.

k) Sabina makes $24,000 a year, while Clara makes only $16,000.