13
THE AREA OF A CIRCLE
The method of rearranging
THE AREA A OF A CIRCLE is
| A = | πr2 or | π 4 |
D2 |
where r is the radius of the circle, and D is the diameter.
The equivalent of that formula was known in ancient times. How did they know it? Very likely from the method of rearranging. (See P. Beckmann, A History of Pi, Barnes & Noble, 1993.) For we know that the area of a rectangle is base times height. Therefore, if we can cut a figure up, and then rearrange the pieces into the form of a rectangle, then we can know the area of that figure
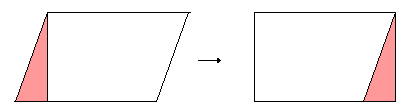
Upon moving the shaded triangle to the other side of the parallelogram, it becomes a rectangle with equal base and height. Therefore we now see that the area of a parallelogram is also base times height.
Let us now try to do the same with a circle.
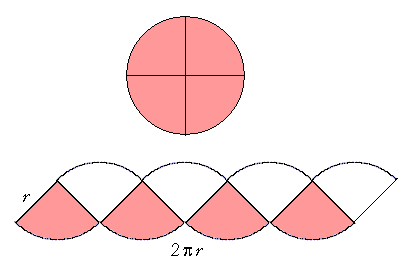
We will first cut it up into four equal sectors, and then arrange them as shown above. In the space between each sector, we draw an equal arc. The resulting figure then begins to resemble a parallelogram Its side is r, and its "base" is equal to the circumference of the circle, 2πr.
The area of that figure is twice the area of the circle.
If we now divide the circle into many more sectors,
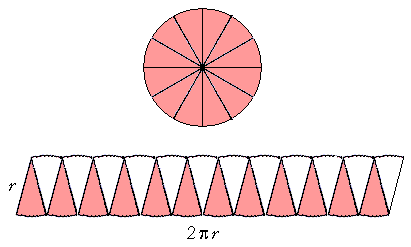
the rearranged figure begins to resemble a parallelogram more closely -- and the side r becomes almost a vertical line.
The area of that figure is, again, twice the area of the circle.
If we now take an extremely large number of sectors, then the side r will become indistinguishable from a vertical line --
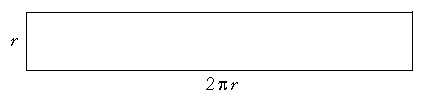
-- and the figure itself will be indistinguishable from a rectangle whose base is 2πr and whose side is r.
Since the area of that rectangle is twice the area of the circle, then the area of the circle is half the base times the height. It will be half of 2πr· r. The area of the circle will be πr2.
In the next Topic, we will see how to find the area of a circle by the method of inscribled polygons.
| Problem. Show that the area of a circle is | π 4 |
D2. |
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| A = πr2 = π( | D 2 |
)2 = π | D2 4 |
= | π 4 |
D2 |
So much for the formula. Now the question is: How can we find a value for π?
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com