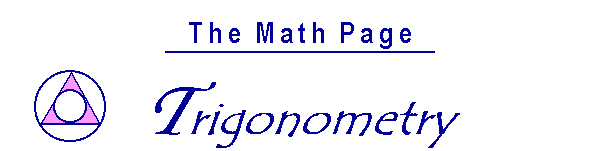
14
EVALUATING π
The ratio of a chord to the diameter
π IS THE RATIO of the circumference of a circle to the diameter. (Topic 2.) But how shall we compare a curved line to a straight line? The answer is that we cannot do it directly. We can only relate straight lines to straight lines, and so we must approximate a curved line by a series of straight lines. In this case, we approximate the circle by an inscribed polygon or a circumscribed polygon.
The perimeter of the inscribed polygon will be less than the circumference of the circle, while the perimeter of the circumscribed polygon will be greater. We can then form the ratio of each perimeter to the diameter. That will produce a lesser and a greater approximation to π.
In the third century B. C., Archimedes of Syracuse considered incribed and circumumscribed polygons of 96 sides. He proved that π is more than ![]() , but less than
, but less than ![]() .
.
![]() < π <
< π < ![]() .
.
In modern decimals:
3.140845 < π < 3.142857
Here is the procedure.
An inscribed polygon
Each side of an inscribed polygon is a chord of the circle. The perimeter of the polygon -- the approximation to the circumference -- will be the sum of all the chords. From the following theorem we are able to evaluate π.
The ratio of a chord of a circle to the diameter
is given by the sine of half the central angle
that the chord subtends.
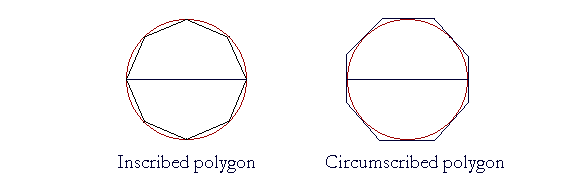
We say that a chord subtends -- literally, stretches under -- a central angle.
Thus if AB is a chord of a circle, and CD the diameter, then
| AB CD |
= sin | θ 2 |
. |
Before proving this theorem, let us give some examples.
Example 1. A chord subtends a central angle of 100°. What ratio has the chord to the diameter?
Answer. According to the theorem,
| Chord Diameter |
= sin ½(100°) |
| Chord Diameter |
= sin 50° |
| Chord Diameter |
= .766, from the Table. |
This means that the chord is 766 thousandths -- or a bit more than three fourths -- of the diameter.
Problem 1. What ratio to the diameter has a chord that subtends a central angle of 60°?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
| Chord Diameter |
= sin ½(60°) = sin 30° = ½ |
This chord is half of the diameter. This chord is equal to the radius!
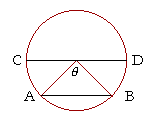
Example 2. A regular polygon of 8 sides is inscribed in a circle. What central angle does each side subtend? What ratio has each side to the diameter? What ratio has the entire perimeter to the diameter?
Answer. Since the polygon has 8 sides, then each central angle is an eighth of the entire circle, that is, an eighth of 360°. 360° ÷ 8 = 45°.
Next,
| Chord Diameter |
= sin ½(45°) |
| Chord Diameter |
= sin 22.5° |
| Chord Diameter |
|
As for the entire perimeter, it is made up of 8 such chords. Therefore, the ratio of the perimeter to the diameter will be
8 × .383 = 3.064
This is an approximation to π. For,
| π | = | Circumference Diameter |
Perimeter Diameter |
The approximation is not a very good one, because we have approximated the circumference with a polygon of only 8 sides.
Problem 2. Let a regular polygon of 20 sides be inscribed in a circle.
a) Each side subtends what central angle? 360° ÷ 20 = 18°
b) What ratio has each side to the diameter? (Table)
| Chord Diameter |
= sin ½(18°) = sin 9° = .156 |
| c) | What ratio has the entire perimeter to the diameter? That is, |
| approximate π. |
The entire perimeter, is made up of 20 such chords. Therefore, the ratio of the perimeter to the diameter will be
20 × .156 = 3.12
We can generalize what we have done as follows. Let us inscribe in a circle a polygon of n sides. Then each side will subtend a central angle θ:
| θ = | 360° n |
Therefore,
| θ 2 |
= | 180° n |
, |
| Chord Diameter |
= sin | 180° n |
Finally, since n such chords approximates the circumference, then the ratio of those n chords to the diameter is an approximation to π:
| π |
180° n |
We shall use this below to prove that the area A of circle is
| A = | π 4 |
D2 | . |
Here is the proof of the ratio of a chord to the diameter.
Theorem. The ratio of a chord of a circle to the diameter is given by the sine of half the central angle that the chord subtends.
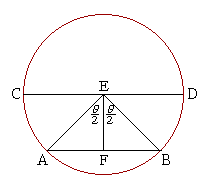
Let E be the center of a circle with chord AB, diameter CD, and central angle AEB, which we will call θ; then
| AB CD |
= sin | θ 2 |
. |
Draw EF so that it bisects angle θ. Then EF is also the perpendicular bisector of AB,
because EA and EB are radii, and so triangle AEB is isosceles (Theorem 2).
Therefore,
| AF | = | ½ AB | . |
| And since EA is a radius, | |||
| EA | = | ½ CD | . |

Now,
| AF EA |
= | sin | θ 2 |
. |
| That is, | ||||
| ½ AB ½ CD |
= | sin | θ 2 |
. |
| Therefore on multiplying both terms by 2, | ||||
| AB CD |
= | sin | θ 2 |
. |
| Chord Diameter |
= | sin | θ 2 |
. |
This is what we set out to prove.
In the previous Lesson, we saw how to know that area by the method of rearranging. Here, we will prove the formula by means of inscribed polygons.
Theorem. The area A of a circle is
| A = | πr2 or | π 4 |
D2 |
where r is the radius of the circle, and D is the diameter.
Proof. Let a regular polygon of n sides be inscribed in a circle of radius r, and let s be the length of each side.
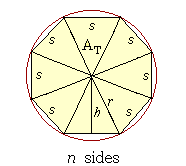
Let us divide the polygon into n isosceles triangles, and let us denote the area of each triangle by AT. Then the area of those n triangles will approximate the area of the circle.
Now the area of each triangle is half the base s times the height h.
AT = ½sh . . . . . . . (1)
We will now express both s and h in terms of the radius r, and then substitute those expressions in line (1).
As we saw above, each chord s subtends a central angle of ![]() .
.
Since the side of each isosceles triangle is the radius r, then h/r is the cosine of half that central angle:
| h r |
= cos ½ | 360° n |
= cos | 180° n |
or,
| h = r cos | 180° n |
. . . . . . . . (2) |
Also, in each isosceles triangle,
| s/2 r |
= sin | 180° n |
so that
| s = 2r sin | 180° n |
. . . . . . . . (3) |
Upon substituting lines (3) and (2) into line (1), we have
| AT = ½sh | = | ½· 2r sin | 180° n |
· r cos | 180° n |
| AT = ½sh | = | r2 sin | 180° n |
· cos | 180° n |
That is the area of one of the triangles. The area A of the entire circle is approximated by all n triangles:
| A = nAT | = | n · r2 sin | 180° n |
· cos | 180° n |
But we have seen that
| n sin | 180° n |
π. |
Therefore, finally,
| A |
180° n |
. . . . . . . . (4) |
Suppose now that the number of sides n is an enormously large number -- more than the number of stars in a million galaxies![]() Then the polygon will "exhaust" the circle. The central angle
Then the polygon will "exhaust" the circle. The central angle ![]() (line 4) will be indistinguishable from 0°. We will have
(line 4) will be indistinguishable from 0°. We will have
A = πr2 cos 0°.
But cos 0° = 1. Therefore,
A = πr2.
| And on replacing r2 with ( | D 2 |
)2 = | D2 4 |
, |
| A | = | π 4 |
D2. |
Which is what we wanted to prove.
When n is an extremely large number, then in the language of calculus, "The limit as n becomes infinite of ![]() is 0°."
is 0°."
Next Topic: Analytic trigonometry: The Unit Circle
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com