12
THE LAW OF SINES
This is a topic in traditional trigonometry. It does not come up in calculus.
THE LAW OF SINES allows us to solve triangles that are not right-angled, and are called oblique triangles. It states the following:
The sides of a triangle are to one another
in the same ratio as the sines of their opposite angles.
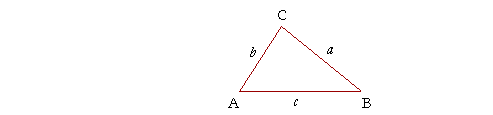
a : b : c = sin A : sin B : sin C.
Specifically, side a is to side b as the sine of angle A is to the sine of angle B.
| a b |
= | sin A sin B |
. |
Similarly,
| b c |
= | sin B sin C |
. |
And so on, for any pair of sides and their opposite angles.
The law of sines is a theorem about the geometry of any triangle. As any theorem of geometry, it can be enunciated. The algebraic statement of the law --
| sin A a |
= | sin B b |
= | sin C c |
-- cannot be verbalized. sin A moreover, which is a number, does not have a ratio to a, which is a length.
Secondly, to prove that algebraic form, it is necessary to state and prove it correctly geometrically, and then transform it algebraically.
Example 1. a) The three angles of a triangle are 40°, 75°, and 65°. In what ratio are the three sides? Sketch the figure and place the ratio numbers.
Solution. To find the ratios of the sides, we must evaluate the sines of their opposite angles. From the Table,
sin 40° = .643
sin 75° = .966
sin 65° = .906
These are the ratios of the sides opposite those angles:
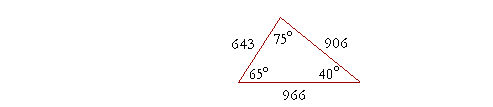
Notice that we may express the ratios as ratios of whole numbers; we may ignore the decimal points. Why? Because we have multiplied each side by the same number, namely 1000. (The theorem of the same multiple.)
b) When the side opposite the 75° angle is 10 cm, how long is the side opposite the 40° angle?
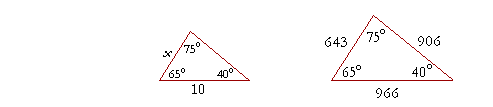
Solution. Let us call that side x. Now, according to the Law of Sines, in every triangle with those angles, the sides are in the ratio 643 : 966 : 906. Therefore,
| x 10 |
= | 643 966 |
|
| x | = | 10· | 643 966 |
With the aid of a calculator,
x![]() 6.656 cm.
6.656 cm.
Problem 1. The three angles of a triangle are A = 30°, B = 70°, and C = 80°.
| a) | In what ratio are the three sides? Sketch the triangle and place those ratio numbers. (Table) |
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
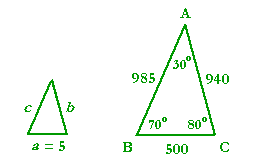
sin 30° = .500
sin 70° = .940
sin 80° = .985
| b) | If side a = 5 cm, find sides b and c. |
In every triangle with those angles, the sides are in the ratio 500 : 940 : 985. But the side corresponding to 500 has been divided by 100. Therefore, each side will be divided by 100. Side b will equal 9.4 cm, and side c = 9.85 cm.
The sine of an obtuse angle
The trigonometric functions (sine, cosine, etc.) are defined in a right triangle in terms of an acute angle. What, then, shall we mean by the sine of an obtuse angle ABC?

The sine of an obtuse angle is defined to be the sine of its supplement.
For example,
| sin 120° | = | sin 60° | = | 2 |
. |
(Topic 4.)
To see why we make this definition, let ABC be an obtuse angle, and
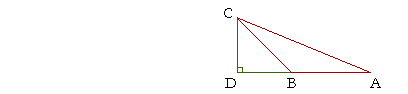
draw CD perpendicular to AB extended.
Then we define the sine of angle ABC as follows:
| sin ABC = | CD CB |
. |
But that is the sine of angle CBD -- opposite-over-hypotenuse. And angle CBD is the supplement of angle ABC. So, by the sine of an obtuse angle we mean the sine of its supplement.
For example,
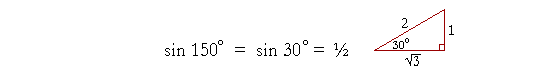
| sin 110° | = | sin (180° − 110°) |
| = | sin 70° | |
| = | .940, from the Table. |
Problem 1. Evaluate the following:
a) sin 135°
= sin 45° = ½![]() (Topic 4, Example 1)
(Topic 4, Example 1)
b) sin 127°
= sin (180° − 127°) = sin 53° = .799
(From the Table)
Problem 2.
a) The three angles of a triangle are 105°, 25°, and 50°. In what ratio
a) are the sides? Sketch the triangle.
| sin 105° | = sin (180° - 105°) |
| = sin 75° | |
| = .966, from the Table. | |
| sin 25° | = .423 |
| sin 50° | = .766 |
Therefore, the sides opposite those angles are in the ratio
966 : 423 : 766
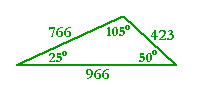
b) If the side opposite 25° is 10 cm, how long is the side opposite 50°?

|
x 10 |
= |
766 423 |
. |
With the aid of a calculator, this implies:
| x | = | 10· |
766 423 |
18.1 cm |
The ambiguous case
The so-called ambiguous case arises from the fact that an acute angle and an obtuse angle have the same sine. If we had to solve
sin x = ½![]() ,
,
for example, we would have
x = 45° or x = 135°.
In the following example, we will see how this ambiguity could arise.
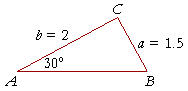
In triangle ABC, angle A = 30°, side a = 1.5 cm, and side b = 2 cm. Let us use the law of sines to find angle B.
| sin B sin 30° |
= | 2 1.5 |
|
| Since sin 30° = ½ (Topic 4, Example 2), | |||
| sin B | = | ½· | 20 15 |
| = | 10 15 |
||
| = | 2 3 |
||
| .666 | |||
On inspecting the Table for the angle whose sine is closest to .666, we find
B![]() 42°.
42°.
But the sine of an angle is equal to the sine of its supplement. That is, .666 is also the sine of 180° − 42° = 138°.
This problem has two solutions. Not only is angle CBA a solution,
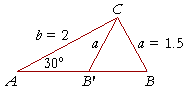
but so is angle CB'A, which is the supplement of angle CBA. (We can see that it is the supplement by looking at the isosceles triangle CB'B; angle CB'A is the supplement of angle CB'B, which is equal to angle CBA.)
Given two sides of a triangle a, b, then, and the acute angle opposite one of them, say angle A, under what conditions will the triangle have two solutions, only one solution, or no solution?
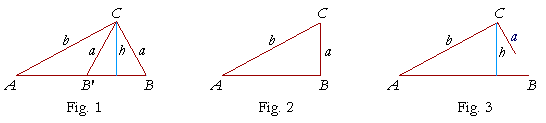
Let us first consider the case a < b. Upon applying the law of sines, we arrive at this equation:
| 1) | sin B | = | sin A· | b a |
. |
| Now, since | h b |
= | sin A | , where h is the height of the triangle (Fig. 1), |
then
b sin A = h.
On replacing this in the right-hand side of equation 1), it becomes
| sin B = | h a |
. |
There are now three possibilities:

| h a |
< | 1, which implies h < a (Fig. 1), |
| h a |
= | 1, which implies h = a (Fig. 2), |
| h a |
> | 1, which implies h > a (Fig. 3). |
In the first of these -- h or b sin A < a -- there will be two triangles.
In the second -- h or b sin A = a -- there will be one right-angled triangle.
And in the third -- h or b sin A > a -- there will be no solution.
Example 2. Let a = 2 cm, b = 6 cm, and angle A = 60°. How many solutions are there for angle B?
Answer. We must calculate b sin A. If it is less than a, there will be two solutions. If it is equal to a, there will be one solution. And if it is greater than a, there will be no solution.
| Now, sin 60° = | 2 |
. (Topic 4.) Therefore, |
| b sin A | = 6· | 2 |
= | 3 |
. |
Since a = 2, then b sin A > a. (![]()
![]() 1.732).
1.732).
There is no solution.
Finally, we will consider the case in which angle A is acute, and a > b.
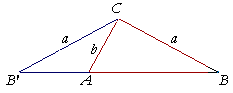
In this case, there is only one solution, namely, the angle B in triangle CBA. For, in triangle CAB', the angle CAB' is obtuse.
Problem 3. In each of the following, find the number of solutions.
a) Angle A = 45°, a = ![]() , b = 2.
, b = 2.
Since ![]() < 2, this is the case a < b. sin 45° =
< 2, this is the case a < b. sin 45° = ![]() /2. Therefore, b sin A = 2
/2. Therefore, b sin A = 2![]() /2 =
/2 = ![]() , which is equal to a. There is therefore one solution: angle B is a right angle.
, which is equal to a. There is therefore one solution: angle B is a right angle.
b) Angle A = 45°, a = 1.8, b = 2.
Again, a < b. b sin A = 2![]() /2 =
/2 = ![]() , which is less than a. Therefore there are two solutions.
, which is less than a. Therefore there are two solutions.
c) Angle A = 45°, a = 2, b = 1.5.
Here, a > b. Therefore there is one solution.
d) Angle A = 45°, a = 1.4, b = 2.
a < b. b sin A = 2![]() /2 =
/2 = ![]() , which is greater than a. Therefore there are no solutions.
, which is greater than a. Therefore there are no solutions.
Proof of the law of sines
The sides of a triangle are to one another in the same ratio as the sines
of their opposite angles.
Since the trigonometric functions are defined in terms of a right-angled triangle, then it is only with the aid of right-angled triangles that we can prove anything![]()
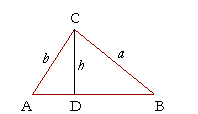
In triangle ABC, then, draw CD perpendicular to AB. Then CD is the height h of the triangle. The height now separates triangle ABC into two right triangles, CDA and CDB.
We will now show that
| sin A sin B |
= | a b |
. |
Now, in triangle CDA,
| sin A = | h b |
. |
While in triangle CDB,
| sin B = | h a |
. |
Therefore,
| sin A sin B |
= | h/b h/a |
= | h b |
· | a h |
= | a b |
. |
This is what we wanted to prove.
In the same way, we could prove that
| sin B sin C |
= | b c |
and so on, for any pair of angles and their opposite sides.
Next Topic: The area of a circle
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com