The Topics | Home

Proof of the sum formulas

Theorem.	sin ( + β)	=	sin cos β + cos sin β
and
	cos ( + β)	=	cos cos β − sin sin β.

Proof.   Let the straight line AB revolve to the point C and sweep out the

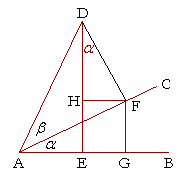
angle , and let it continue to D and sweep out the angle β;

draw DE perpendicular to AB.

Then we are to determine sin ( + β), which is

ED DA

,

and cos ( + β), which is

AE DA

.

Note: The value of a trigonometric function is a number, namely the number that represents the ratio of two lengths. Throughout the proof, then, we will consider AE and DA not only as lengths, but also as the numbers that are their measures. Therefore the usual properties of arithmetic will apply.

Draw DF perpendicular to AC,

draw FG perpendicular to AB,

and draw FH perpendicular to ED.

Then angle HDF is equal to angle .

For, since the straight line AC crosses the parallel lines HF, AB, it makes the alternate angles equal (Theorem 8);

therefore angle HFA is equal to angle .

And by the construction, angle DFH is the complement of angle HFA;

therefore angle HDF (the complement of DFH) is also equal to angle .

Now,

	ED = GF + HD.
Therefore, on dividing by DA,
sin ( + β)  =	ED DA	=	GF DA	+	HD DA

And on both dividing and multiplying by AF and FD

	=	GF AF	AF DA	+	HD FD	FD DA	Multiplying   fractions.
	=	sin cos β + cos sin β.

Next,

	EA = GA − FH.
Therefore,
cos ( + β)  =	EA AD	=	GA AD	−	FH AD

	=	GA AF	AF AD	−	FH DF	DF AD
	=	cos cos β − sin sin β.

This is what we wanted to prove.

The difference formulas can be proved from the sum formulas, by replacing +β with +(−β), and using these identities:

cos (−β) = cos β 

sin (−β) = −sin β.

Topic 16

Back to Trigonometric identities

Copyright © 2021 Lawrence Spector

Questions or comments?

E-mail:  teacher@themathpage.com