20
TRIGONOMETRIC IDENTITIES
Tangent and cotangent identities
AN IDENTITY IS AN EQUALITY that is true for any value of the variable. (An equation is an equality that is true only for certain values of the variable.)
In algebra, for example, we have this identity:
(x + 5)(x − 5) = x2 − 25.
The significance of an identity is that, in calculation, we may replace either member with the other. We use an identity to give an expression a more convenient form. In calculus and all its applications, the trigonometric identities are of central importance.
On this page we will present the main identities. The student will have no better way of practicing algebra than by proving them. Links to the proofs are below.
Reciprocal identities
| sin θ | = | 1 csc θ |
csc θ | = | 1 sin θ |
|
| cos θ | = | 1 sec θ |
sec θ | = | 1 cos θ |
|
| tan θ | = | 1 cot θ |
cot θ | = | 1 tan θ |
|
Again, in calculation we may replace either member of the identity with the other. And so if we see "sin θ", then we may, if we wish, replace it with "![]() "; and, symmetrically, if we see "
"; and, symmetrically, if we see "![]() " then we may replace it with "sin θ".
" then we may replace it with "sin θ".
Problem 1. What does it mean to say that csc θ is the reciprocal of sin θ ?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
It means that their product is 1.
sin θ csc θ = 1.
Problem 2. Evaluate
tan 30° csc 30° cot 30°.
| tan 30° csc 30° cot 30 ° | = | tan 30° cot 30 ° csc 30 ° |
| = | 1 · csc 30 ° | |
| = | 2. | |
Tangent and cotangent identities
| tan θ = | sin θ cos θ |
cot θ = | cos θ sin θ |
The proof is here.
Example 1. Show: tan θ cos θ = sin θ.
Solution: The problem means that we are to write the left-hand side, and then show, through substitutions and algebra, that we can transform it to look like the right hand side.
We begin:
| = | on applying the tangent identity, | ||
| = | on canceling the cos θ 's. | ||
We have arrived at the right-hand side.
| a) | sin2θ + cos2θ | = | 1. |
| b) | 1 + tan2θ | = | sec2θ |
| c) | 1 + cot2θ | = | csc 2θ |
| a') | sin2θ | = | 1 − cos2θ. |
| cos2θ | = | 1 − sin2θ. | |
These are called Pythagorean identities, because, as we will see in their proof, they are the trigonometric version of the Pythagorean theorem.
The two identities labeled a') -- "a-prime" -- are simply different versions of a). The first shows how we can express sin θ in terms of cos θ; the second shows how we can express cos θ in terms of sin θ.
Note: sin2θ -- "sine squared theta" -- means (sin θ)2.
Problem 3. A 3-4-5 triangle is right-angled.
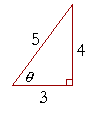
a) Why?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
It satisfies the Pythagorean theorem.
b) Evaluate the following:
| sin2θ | = | 16 25 |
cos2θ | = | 9 25 |
sin2θ + cos2θ | = | 1. |
Example 2. Show:
| Solution. Again, we are to transform the left-hand side into the right. We begin: | ||
| Reciprocal identities | ||
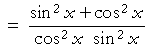 |
on adding the fractions | |
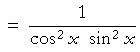 |
Pythagorean identities | |
| Reciprocal identities | ||
That is what we wanted to show.
| sin (α + β) | = | sin α cos β + cos α sin β |
| sin (α − β) | = | sin α cos β − cos α sin β |
| cos (α + β) | = | cos α cos β − sin α sin β |
| cos (α − β) | = | cos α cos β + sin α sin β |
Note: In the sine formulas, + or − on the left is also + or − on the right. But in the cosine formulas, + on the left becomes − on the right; and vice-versa.
Since these identities are proved directly from geometry, the student is not normally required to master the proof. However, all the identities that follow are based on these sum and difference formulas. The student should definitely know them.
Here is the proof of the sum formulas.
Example 3. Evaluate sin 15°.
Example 4. Prove:
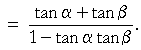 |
||||
| Solution. | 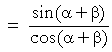 |
Tangent identity | ||
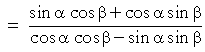 |
Formulas | |||
| We will now construct tan α by dividing the first term in the numerator by cos α cos β. But then we must divide every term by cos α cos β: | ||||
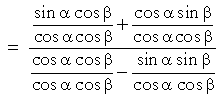 |
||||
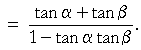 |
||||
That is what we wanted to prove.
Double-angle formulas
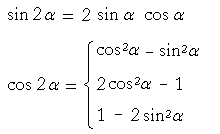
There are three versions of cos 2α. The first is in terms of both cos α and sin α. The second is in terms only of cos α. The third is in terms only of sin α
| Example 5. Show: sin 2α |
| Solution. | sin 2α | = 2 sin α cos α | Formulas | |
| We will now construct tan α by dividing by cos α. But to preserve the equality, we must also multiply by cos α. | ||||
| Lesson 5 of Algebra | ||||
| Reciprocal identities | ||||
| Pythagorean identities | ||||
That is what we wanted to prove.
| Example 6. Show: | 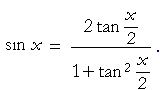 |
| Solution. | sin x | 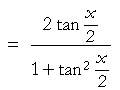 |
—according to the previous identity with α = ![]() .
.
Half-angle formulas
The following half-angle formulas are inversions of the double-angle formulas, because α is half of 2α.
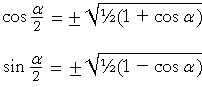
The plus or minus sign will depend on the quadrant. Under the radical, the cosine has the + sign; the sine, the − sign.
| Example 7. Evaluate cos | π 8 |
. |
| Solution. Since | π 8 |
is half of | π 4 |
, then according to the |
| half angle formula: | ||||
| Example 8. Derive an identity for tan | α 2 |
. |
| Solution. | tan | α 2 |
= | Tangent identity | ||
| = | 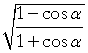 |
Half angle formulas | ||||
| = | 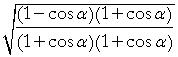 |
|||||
| = | 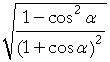 |
Lesson 19 of Algebra | ||||
| = | 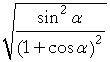 |
Pythagorean identity a' | ||||
| = | ||||||
| = | ||||||
on dividing both numerator and denominator by cos α.
Products as sums
| a) | sin α cos β | = | ½[sin (α + β) + sin (α − β)] | |
| b) | cos α sin β | = | ½[sin (α + β) − sin (α − β)] | |
| c) | cos α cos β | = | ½[cos (α + β) + cos (α − β)] | |
| d) | sin α sin β | = | −½[cos (α + β) − cos (α − β)] | |
| e) | sin A + sin B | = | 2 sin ½ (A + B) cos ½ (A − B) |
| f) | sin A − sin B | = | 2 sin ½ (A − B) cos ½ (A + B) |
| g) | cos A + cos B | = | 2 cos ½ (A + B) cos ½ (A − B) |
| h) | cos A − cos B | = | −2 sin ½ (A + B) sin ½ (A − B) |
In the proofs, the student will see that the identities e) through h) are inversions of a) through d) respectively, which are proved first. The identity f) is used to prove one of the main theorems of calculus, namely the derivative of sin x.
The student should not attempt to memorize these identities. Practicing their proofs -- and seeing that they come from the sum and difference formulas -- is enough.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com