1
THE NATURAL NUMBERS
MATHEMATICS IS NOT ONLY about numbers, it is about things that are not numbers; for example, length; the distance from here to there,
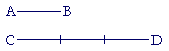
from A to B. Now a length is not a number, yet we describe lengths by saying that they are like numbers. For if CD is made up of three segments equal to AB, then we say,
AB is to CD as 1 is to 3.
And if AB were 1 centimeter, we would say that CD is 3 centimeters.
That is, we can say that CD is "three times" AB, and "three times" is the name of the ratio -- the relationship -- of CD to AB. The eventual question will be:
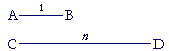
If AB is the unit of length, and CD is any length, will we always be able to name their ratio, that is, express it in words? Will we always be able to name a number n such that, proportionally,
AB is to CD as 1 is to n?
That number will be called a real number, which is a number we will need for measuring rather than counting. We will see that there will be problems. At the root of the problem is the difference between arithmetic and geometry.
The natural numbers
A unit is that form in accordance with which each thing that we perceive to exist we say is one, and call by a name.
(After Euclid, Book VII, Definition 1.)
One apple, one orange, one person.
A natural number is composed of distinct, indivisible units of the same kind.
![]()
The people in the room, the electrons in an atom, the fingers on your hand. Each unit is indivisible: You cannot take half of any one. If you do, it will not be that unit—it will not deserve the same name—any more. Half a person is not also a person.
Every language has its names for the natural numbers. The English names are the familiar "One, two, three, four," and so on. Their numerals are "1, 2, 3, 4." Like the names, they stand for the numbers, and it is with those that we count and calculate; hence it has become common to call the numerals themselves "numbers." Throughout history there have been many ways of representing numbers. The student is surely familiar with the Roman numerals: I, V, X, and so on.
The natural number however is the idea of the actual collection of units, /////, which we could represent by strokes, or dots, or a line divided into equal parts. For there is no "5" apart from five units, even though we do not say the word units.
We will see that we can always put into words how any two natural numbers are related. That relationship is called their ratio.
Cardinal and ordinal
The counting-names have two forms: cardinal and ordinal. The names of the cardinal numbers are
One, two, three, four,
and so on. They answer the question How many?
The names of the ordinal numbers are
First, second, third, fourth,
and so on. They answer the question Which one?
We will now see that the ordinal numbers express division into equal parts. They will answer the question, Which part?
Parts of natural numbers
If a smaller number is contained in a larger number an exact number of times, then we say that the smaller number is a part of the larger. (That is called an aliquot part.) Equivalently, the larger number is a multiple of the smaller.
Consider these first few multiples of 5:
5, 10, 15, 20, 25, 30.
5 is the first multiple of 5. 10 is the second; 15, the third; and so on.
5 is a part of each of its multiples except itself. It is a part of 10, of 15, of 20, and so on.
Now, since 15 is the third multiple of 5, we say that 5 is the third part of 15. We use that same ordinal number to name the part.
The ordinal number "third" names which part of fifteen 5 is.
5 is the fourth part of 20; it is the fifth part of 25; the sixth part of 30. And so on.
5 is which part of 10? We do not say the second part. We say half. 5 is half of 10.
It is extremely important to understand that we are not speaking here of proper fractions -- numbers that are less than 1 and that we need for measuring. We are explaining how the ordinal numbers -- third, fourth, fifth, and so on -- name the parts of the cardinal numbers. Those ordinal names of the parts are logically prior to the names of the fractions, as we will see. (Why do we call the number we write as 1 over 3 "one-third"? Because 1 is the third part of 3. And that fraction is the third part of 1.)
Note that 5 is not a part of itself. There is no such thing as the first part.
So, with the exception of the name half, we name each part with an ordinal number. The ordinal number names which part.
(For more details, see Skill in Arithmetic, Lesson 15.)
Problem 1.
a) Write the first five multiples of 6.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
6 12 18 24 30
b) 6 is which part of each one of those (except 6)?
6 is half of 12; the third part of 18; the fourth part of 24; the fifth part of 30.
Problem 2. Complete the following with the word multiple or part.
a) A larger number is a multiple of a smaller.
b) A smaller number is a part of a larger.
c) 15 is the fifth multiple of 3, is the same as saying that 3 is the fifth
c)
part of 15.
d) We say that 4 is the third part of 12, because 12 is the third multiple
d) of 4.
e) 40 is eight times 5, therefore 5 is called the eighth part of 40.
f) Every number is a certain part of each of its multiples.
g) A number is divisible by 9, is the same as saying that the number is a
g) multiple
of 9.
Problem 3.
a) Write all the divisors of 20.
1, 2, 4, 5, 10, and 20
b) Each divisor, except 20 itself, is which part of 20?
1 is the twentieth part of 20.
2 is the tenth part of 20.
4 is the fifth part of 20.
5 is the fourth part of 20.
10 is half of 20.
Problem 4. 1 is a part of every number. Which part is it of the following?
2 Half. 3 Third. 4 Fourth. 10 Tenth. 79 Seventy-ninth.
100 Hundredth.
Problem 5. What number is each of the following?
| a) The eighth part of 8. 1 | b) The tenth part of 10. 1 | |
| c) The fifth part of 5. 1 | d) The sixth part of 42. 7 | |
| e) The eighth part of 24. 3 | f) The fifth part of 10. 2 | |
| g) The tenth part of 40. 4 | h) The fourth part of 20. 5 | |
| i) The ninth part of 9. 1 | j) The third part of 21. 7 | |
| k) The fifth part of 40. 8 | l) The seventh part of 63. 9 | |
| m) The fourth part of 36. 9 | n) The sixth part of 72. 12 | |
Divisors and parts
Theorem. For every divisor that a number has (except 1), it will have a part with the ordinal name of that divisor.
That is, if a number has a divisor 3, then it will have a third part; if it has a divisor 4, it will have a fourth part; while if it has a divisor 2, then it will have a half.
Example. Into which parts could 50 people be divided?
Answer. Here are all the divisors of 50:
1, 2, 5, 10, 25, 50
Corresponding to each divisor (except 1) there will be a part with the ordinal name of that divisor. Thus, since 2 is a divisor, 50 has a half (which is 25). Since 5 is a divisor, 50 has a fifth part (which is 10). Since 10 is a divisor, 50 has a tenth part (which is 5). Finally, it has a twenty-fifth part (which is 2), and a fiftieth part (which is 1).
These are the only parts into which 50 people could be divided. You cannot take a third of 50 people. 50 does not have a divisor 3.
Problem 6. Which numbers have a sixth part?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Only those numbers that are divisible by 6. They are the multiples of 6:
6, 12, 18, 24, 30, etc.
The sixth part of 6 is 1; the sixth part of 12 is 2; the sixth part of 18 is 3; and so on.
Problem 7.
a) Name all the divisors of 32. Name each part that 32 has.
Divisors: 1 2 4 8 16 32
32 has a half, a fourth part, an eighth part, a sixteenth part, and a thirty-second part.
b) Name each part that 13 has.
Only a thirteenth part, which is 1.
c) 10 people could be divided into which parts?
Half, fifths, and tenths.
d) 7 pencils could be divided into which parts?
Sevenths.
Parts, plural
If we divide 15 into three equal parts, that is, into thirds, then the third part of 15 is 5.
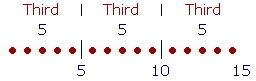
But each 5 is a third part of 15. Therefore, two 5's -- 10 --are two third parts of 15. Or simply two thirds.
Those words, "two thirds," are to be taken literally, like two apples or two chairs. Two thirds are twice as much as one third. Count them:
One Third, two Thirds. 5, 10.
Now, 10 is not a part of 15 because 15 is not a multiple of 10. We say, rather, that it is parts, plural. Two third parts.
Similarly, if we divide 15 into its fifths,
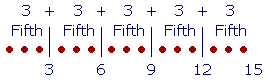
then
3 is the fifth part of 15.
6 is two fifth parts of 15.
9 is three fifth parts of 15. (Count them!)
12 is four fifth parts of 15; or simply four fifths.
And 15 is all five of its fifth parts.
We can state the following theorem:
Theorem. Each number is either a part of a larger number or parts of it.
The following problem will illustrate this. It will illustrate that each number less than 9 is either a part of 9 or parts of 9.
Problem 8.
a) Into which parts can 9 be divided?
Ninths and Thirds.
![]()
b) Each number less than 9 is which part of 9, or which parts of 9?
1 is the ninth part of 9.
2 is two ninths of 9.
3 is three ninths -- and also the third part -- of 9.
4 is four ninths of 9.
5 is five ninths of 9.
6 is six ninths -- and also two thirds -- of 9.
7 is seven ninths of 9.
8 is eight ninths of 9.
Each number less 9, then, is either a part of 9 or parts of it. We can therefore express in words how each of those numbers is related to 9. We can say that 7, for example, is "seven ninths" of 9.
Notice how each number says its name. 7 says its cardinal name "seven." 9 says its ordinal name "ninth."
Problem 9. What relationship has 9 to 10?
![]()
9 is nine tenths of 10.
Next Topic: The ratio of two natural numbers
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2020 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
