Algebraic expressions: Section 2
Question 5. What do we mean by the value of a letter?
The value of a letter is a number. It is the number that will replace the letter when we do the order of operations.
Question 6. What does it mean to evaluate an expression?
It means to replace each letter with its value, and then do the order of operations.
Example 6. Let x = 10, y = 4, z = 2. Evaluate the following.
| a) x + yz | = | 10 + 4· 2 | b) (x + y)z | = | (10 + 4)2 | |
| = | 10 + 8 | = | 14· 2 | |||
| = | 18. | = | 28. | |||
In each case, copy the pattern. Copy the + signs and copy the parentheses ( ). When you come to x, replace it with 10. When you come to y, replace it with 4. And when you come to z, replace it with 2.
Problem 7. Let x = 10, y = 4, z = 2, and evaluate the following.
| a) | x + 2(y + z) = | b) | (x + 2)(y + z) = | ||
| 10 + 2(4 + 2) = 10 + 2· 6 = 10 + 12 = 22. |
(10 + 2)(4 + 2) = 12· 6 = 72 | ||||
| c) | x − 3(y − z) = | d) | (x − 3)(y − z) = | ||
| 10 − 3(4 − 2) = 10 − 3· 2 = 10 − 6 = 4 |
(10 −3)(4 − 2) = 7· 2 = 14 | ||||
| e) | x − y + z = | f) | x − (y + z) = | ||
| 10 − 4 + 2 = 6 + 2 = 8 | 10 − (4 + 2) = 10 − 6 = 4 | ||||
g) x2 − y2 + 3z2 = 100 − 16 + 3· 4 = 100 − 16 + 12 = 84 + 12 =96.
Again, 100 − 16 + 12 does not mean 100 − (16 + 12).
| h) | 10y² + z³ x2 |
= | 10· 16 + 8 100 |
| = | 160 + 8 100 |
||
| = | 168 100 |
||
| = | 1.68 | ||
That is 168 divided by 100. See Lesson 4 of Arithmetic, Question 4.
Question 7. Why is a literal symbol -- x, y, z -- called a variable?
Because its value may vary.
A variable, such as x, is a kind of blank or empty symbol. It is therefore available to take any value we might give it: a positive number or, as we shall see, a negative number; a whole number or a fraction.
Numerical symbols -- 2, 3, 4 -- are called constants. The value of those symbols does not vary.
(See Constants versus variables.)
Problem 8. Two variables. Let the value of the variable y depend
on the value of the variable x as follows:
y = 2x + 4.
Calculate the value of y that corresponds to each value of x:
When x = 0, y = 2· 0 + 4 = 0 + 4 = 4.
When x = 1, y = 2· 1 + 4 = 2 + 4 = 6.
When x = 2, y = 2· 2 + 4 = 4 + 4 = 8.
When x = 3, y = 2· 3 + 4 = 6 + 4 = 10.
When x = 4, y = 2· 4 + 4 = 8 + 4 = 12.
Algebraic expressions
Real problems in science or in business occur in ordinary language. To do such problems, we typically have to translate them into algebraic language.
Problem 9. Write an algebraic expression that will symbolize each of the following.
a) Six times a certain number. 6n, or 6x, or 6m. Any letter will do.
b) Six more than a certain number. x + 6
c) Six less than a certain number. x − 6
d) Six minus a certain number. 6 − x
e) A number repeated as a factor three times. x· x· x = x3
f) A number repeated as a term three times. x + x + x
g) The sum of three consecutive whole numbers. The idea, for example,
g) of 6 + 7 + 8. [Hint: Let x be the first number.]
g)
x + (x + 1) + (x + 2)
h) Eight less than twice a certain number. 2x − 8
i) One more than three times a certain number. 3x + 1
Now an algebraic expression is not a sentence, it does not have a verb, which is typically the equal sign = . An algebraic statement has an equal sign.
Problem 10. Write each statement algebraically.
a) The sum of two numbers is twenty. x + y = 20.
b) The difference of two numbers is twenty. x − y = 20.
c) The product of two numbers is twenty. xy = 20.
d) Twice the product of two numbers is twenty. 2xy = 20.
e) The quotient of two numbers is equal to the sum of those numbers.
| x y |
= x + y. |
Formulas
A formula is an algebraic rule for evaluating some quantity. A formula is a statement.
Example 7. Here is the formula for the area A of a rectangle whose base is b and whose height is h.
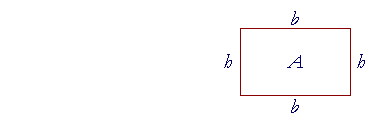
A = bh.
"The area of a rectangle is equal to the base times the height."
And here is the formula for its perimeter P -- that is, its boundary:
P = 2b + 2h.
"The perimeter of a rectangle is equal to two times the base
plus two times the height."
For, in a rectangle the opposite sides are equal.
Problem 11. Evaluate the formulas for A and P when b = 10 in, and h = 6 in.
A = bh = 10· 6 = 60 in2.
P = 2b + 2h = 2· 10 + 2· 6 = 20 + 12 = 32 in.
Problem 12. The area A of trapezoid is given by this formula,
A = ½(a + b)h.
Find A when a = 2 cm, b = 5 cm, and h = 4 cm.
A = ½(2 + 5)4 = ½· 7· 4 = 7· 2 = 14 cm2.
When 1 cm is the unit of length, then 1 cm² ("1 square centimeter") is the unit of area.
Problem 13. The formula for changing temperature in degrees Fahrenheit (F) to degrees Celsius (C) is given by this formula:
| C = | 5 9 |
(F − 32). |
Find C if F = 68°.
Replace F with 68:
| C = | 5 9 |
(68 − 32) = | 5 9 |
· 36 = 5· 4 = 20°. |
| 5 9 |
· 36 means "Five ninths of 36." | Lesson 27 of Arithmetic. |
"One ninth of 36 is 4. So five ninths is five times 4: 20."
Next Lesson: Signed numbers -- Positive and negative
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com