35
SIMULTANEOUS
LINEAR EQUATIONS
Section 2:
Cramer's Rule: The method of determinants
Section 3:
Three equations in three unknowns
THIS LESSON DEPENDS on Lesson 9: Linear equations.
Example 1. Solve simultaneously for x and y:
| x + y | = | 10 |
| x − y | = | 2 |
This means that we must find values of x and y that will solve both equations. We must find two numbers whose sum is 10 and whose difference is 2.
The two numbers, obviously, are 6 and 4:
| 6 + 4 | = | 10 |
| 6 − 4 | = | 2 |
Let us represent the solution as the ordered pair (6, 4).
Now, these two equations --
| x + y | = | 10 |
| x − y | = | 2 |
-- are linear equations (Lesson 33). Hence, the graph of each one is a straight line. Here are the two graphs:
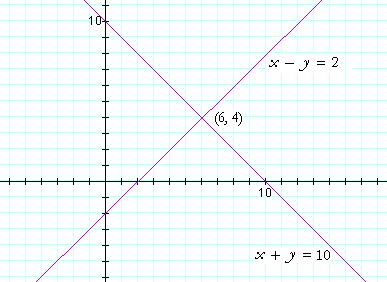
The solution to the simultaneous equations is their point of intersection. Why? Because that coördinate pair solves both equations. (Lesson 33.) That point is the one and only point on both lines.
We speak of a system of simultaneous equations.
Example 2. Solve simultaneously for x and y.
| 2x | + | y | = | 4 |
| x | − | y | = | −1 |
Solution. In this case, the solution is not obvious. Here is a general strategy for solving simultaneous equations:
When one pair of coefficients are negatives of one another,
add the equations vertically, and that unknown will cancel.
We will then have one equation in one unknown, which we can solve.
Upon adding those equations, the y's cancel:
| 2x | + | y | = | 4 |
| x | − | y | = | −1 |
| __________________________________ | ||||
| 3x | = | 3 | ||
| x | = | 3 3 |
||
| x | = | 1. | ||
To solve for y, the other unknown :
Substitute the value of x in one of the original equations.
Upon substituting x = 1 in the top equation:
| 2 · 1 + y | = | 4 |
| y | = | 4 − 2 |
| y | = | 2. |
If we report the solution as an ordered pair, then the solution is (1, 2). Those are the coördinates of the point of intersection of the two lines.
This method of solving simultaneous equations is called the method of addition.
Example 3. Solve the same system of equations by the method of substitution.
| 1) | 2x | + | y | = | 4 |
| 2) | x | − | y | = | −1 |
Here is the method of substitution:
Solve one of the equations for one unknown in terms of the other.
Then, substitute that in the other equation.
That will yield one equation in one unknown, which we can solve.
Let us solve equation 1) for y:
| 1) | y = 4 − 2x | ||
| And now, substitute this for y in equation 2): | |||
| 2) | x − (4 − 2x) | = | −1 |
| This equation has only the unknown x: | |||
| x − 4 + 2x | = | −1 | |
| 3x | = | −1 + 4 | |
| 3x | = | 3 | |
| x | = | 1 | |
| To find y, substitute x = 1 in line 1): | |||
| y | = | 4 − 2 · 1 | |
| y | = | 2. | |
Problem 1 . Solve this system of two equations in two unknowns.
Solve it by the method of addition. Solve it again by the method of substitution.
| x | − | y | = | 2 |
| 2x | + | y | = | 10 |
The method of addition:
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Upon adding those equations, the y's cancel:
| x | − | y | = | 2 |
| 2x | + | y | = | 10 |
| __________________________________ | ||||
| 3x | = | 12 | ||
| x | = | 12 3 |
||
| x | = | 4. | ||
To solve for y:
Substitute x = 4 in either of the original equations; for example, in the bottom equation:
| 2 · 4 + y | = | 10 |
| y | = | 10 − 8 |
| y | = | 2. |
The method of substitution:
| x | − | y | = | 2 |
| 2x | + | y | = | 10. |
Solve the top equation for x:
| 1) x | = | 2 + y |
| Substitute this for x in the bottom equation, and solve that equation for y: | ||
| 2(2 + y) + y | = | 10 |
| 4 + 2y + y | = | 10 |
| 3y | = | 6 |
| y | = | 2. |
To solve for x, substitute y = 2 in Line 1.
| x | = | 2 + 2 |
| x | = | 4. |
Problem 2.
a) What is the graph of two linear equations?
Two straight lines.
b) Where on the graph do we find the solution?
At their point of intersection.
c) illustrate your answer with the equations of Problem 1.
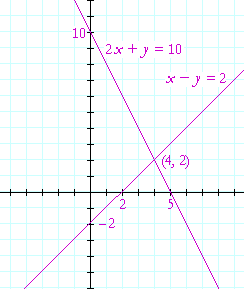
Section 2: More examples. Cramer's Rule: The method of determinants
Next Lesson: Word problems that lead to simultaneous equations
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
