S k i l l
i n
A R I T H M E T I C

Lesson 25

MULTIPLYING FRACTIONS
DIVIDING FRACTIONS

In this Lesson, we will answer the following:

How do we multiply a fraction by a whole number?
How do we multiply a mixed number by a whole number?
How do we multiply a fraction by a fraction?
How do we multiply a mixed number by a mixed number, or a fraction by a mixed number?
Section 2
How do we divide fractions?

3 ×

2
7

("3 times

2
7

"). What does that mean?

According to the meaning of multiplication,

3 ×

2
7

That is,

3 ×

2
7

2 + 2 + 2
7

6
7

We can therefore state the "rule" as follows:

1.	How do we multiply a fraction by a whole number?

	Multiply the numerator by the whole number. Do not change the denominator. If the fraction becomes improper, extract the whole number.

Compare Lesson 19, Question 13.

Example 1.

2 ×

4
9

8
9

Example 2. It takes

2
5

yards of material to make a shirt. How many yards

will it take to make 6 shirts?

Answer. 6 ×

2
5

12
5

= 2

2
5

yards.

2.	How do we multiply a mixed number by a whole number?


	Multiply the whole number and the fraction separately.

2 × 4 = 8.

2 ×

1
3

2
3

When multiplying by a whole number, it is not necessary to change to an improper fraction.

This is exactly what we did to multiply dollars and cents (Lesson 8).

4 × $6.20 = $24 + $.80 = $24 .80

Example 3.

5 × 3

2
11

= 15

10
11

Example 4.

7 × 6

3
5

= 42

21
5

= 42 + 4

1
5

= 46

1
5

Always, if the fraction becomes improper, extract the whole number. (Lesson 19.)

Example 5. Dividing first.

18 ×

2
3

6 × 2

12.

"3 goes into 18 six (6) times. 6 times 2 is 12."

The order of multiplying and dividing does not matter. (Property 3 of division.) If we had multiplied first --

18 ×

2
3

18 × 2
3

-- we would divide by 3 eventually. Dividing first results in multiplying smaller numbers.

Example 6.

20 ×

11
5

4 × 11

44.

"5 goes into 20 four (4) times."

3.	How do we multiply a fraction by a fraction?

	Multiply the numerators and multiply the denominators.

For the meaning of multiplying by a fraction, see the next Lesson.

Example 7.

3
4

7
11

21
44

When multiplying fractions, do not change to a common denominator.

Example 8.

8
9

15
16

If any numerator has a divisor in common with any denominator, then we can cancel that common divisor.

8 and 16 have a common divisor, which is 8 itself. 9 and 15 have a common divisor, 3.

"8 goes into 8 once (1); 8 goes into 16 two (2) times."

"3 goes into 9 three (3) times; 3 goes into 15 five (5) times."

"1 × 5 = 5. 3 × 2 = 6."

Example 9.

1
2

3
4

5
7

15
56

Multiply all the numerators: 1 × 3 × 5 = 15

Multiply all the denominators: 2 × 4 × 7 = 8 × 7 = 56

The time to cancel is before multiplying when the numbers are smaller. If nothing cancels before , as in this example, then the answer is already in its lowest terms.

Example 10.

4
3

9
2

2 is a common divisor of 4 and 2. 3 is a common divisor of 3 and 9.

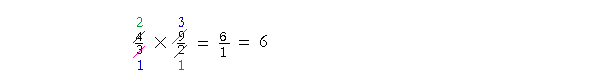
"2 goes into 4 two (2) times; 2 goes into 2 one (1) time."

"3 goes into 3 one (1) time; 3 goes into 9 three (3) times."

"2 × 3 = 6. 1 × 1 = 1."

A fraction with denominator 1 (

6
1

) is simply the numerator. It is not

necessary to say "1 goes into 6 six times."

Here is another example:

5
1

= 5

Example 11.

4 ×

5
6

We may cancel before multiplying 4 × 5:

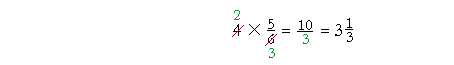
"2 goes into 4 two (2) times."

"2 goes into 6 three (3) times."

"2 × 5 = 10; over 3."

We would cancel after multiplying 4 × 5; and so we may cancel before. Again, the advantage of canceling first is that we work with smaller numbers.

4.	How do we multiply a mixed number by a mixed number, or a fraction by a mixed number?

	Change the mixed numbers to improper fractions (Lesson 19).

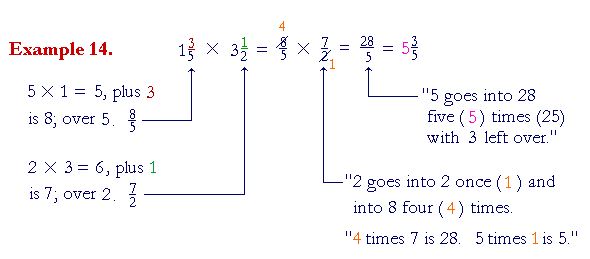
This is the only place in arithmetic where it is necessary to change to an improper fraction.

Example 13.

2 × 4

1
3

= 8

2
3

It is not necessary to change to an improper fraction. When multiplying by a whole number, multiply the whole number times the whole number, and multiply the whole number times the numerator.

The following is a ratio and proportion problem. It depends on understanding mixed ratio, Lesson 17.

Example 14. If 6 workers can paint 8 rooms in 10 hours, how long will it take 15 workers to paint 14 rooms?

Solution. We must find out how many rooms 15 workers could paint in ONE hour. We will see that it turns out to be 2. Therefore, since they can paint 2 rooms in 1 hour, then to paint 14 rooms will require 7 times as long: 7 hours.

To begin, how many rooms can 6 workers paint in ONE hour?

Since they can paint 8 rooms in 10 hours, then in 1 hour they can paint

8
10

4
5

of a room.

(That is the number of rooms per hour. Lesson 10.)

Next, what ratio has 15 workers to 6?

15
6

= 2

3
6

= 2½.

There are 2½ times as many workers. Therefore in 1 hour, they will be able to paint 2½ times as many rooms.