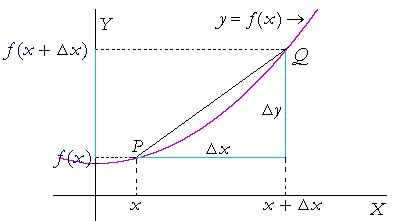CALCULUS IS APPLIED TO THINGS that do not change at a constant rate. Velocity due to gravity, births and deaths in a population, units of y for each unit of x. The values of the function called the derivative will be that varying rate of change.

Now, since we consider x to be the independent variable and y the dependent, then any change Δx in the value of x, will result in a change Δy in the value of y. In a straight line, the rate of change -- so many units of y for each unit of x -- is constant, and is called the slope of the line.

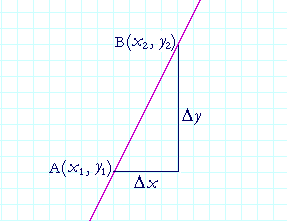
The derivative

The slope of a straight line is this number:

Δy
Δx

Change in y-coördinate
Change in x-coördinate

(Topic 8 of Precalculus.)

A straight line has one and only one slope; one and only one rate of change.

If x represents time, for example, and y represents distance, then a

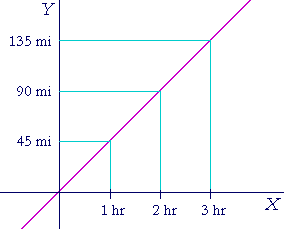
The derivative

straight line graph that relates them indicates constant speed. 45 miles per hour, say -- at every moment of time.

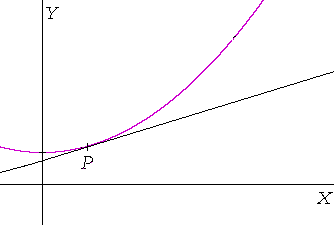
The slope of a tangent line to a curve

Calculus however is concerned with rates of change that are not constant.

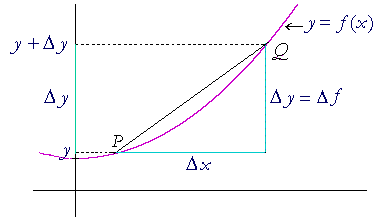
If this curve represents distance Y versus time X, then the rate of change -- the speed -- at each moment of time is not constant. The question that calculus asks is: "What is the rate of change at exactly the point P ?" The answer will be the slope of the tangent line to the curve at that point. And the method for finding that slope -- that number -- was the remarkable discovery by both Isaac Newton (1642-1727) and Gottfried Leibniz (1646-1716). That is the method for finding what is called the derivative.

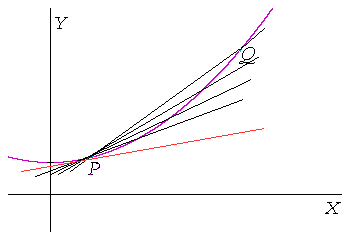
A secant to a curve

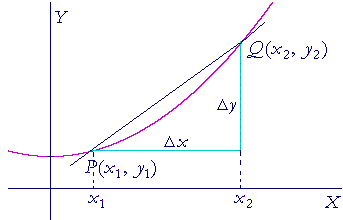
The derivative

A tangent is a straight line that just touches a curve. A secant is a straight line that cuts a curve. Hence, consider the secant line that cuts the curve at points P and Q. Then the slope of that secant is

Δy
Δx

But once again, the question calculus asks is: How is the function changing exactly at x₁?

What is the slope of the tangent to the curve at P?

We cannot however evaluate exactly at P -- because Δy and Δx would then both be 0, and the value of would be completely ambiguous.

Therefore we will consider shorter and shorter distances Δx, which will result in a sequence of secants --

-- a sequence of slopes. And we will define the tangent at P to be the limit of that sequence of slopes.

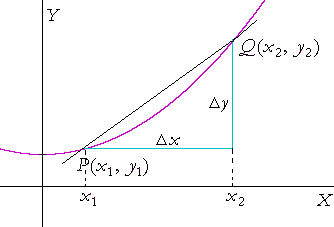
The derivative

That slope, that limit, will be the value of what we will call the derivative.

The difference quotient

Let y = f(x) be a continuous function, and let the coördinates of a fixed point P on the graph be (x, f(x)). (Topic 4 of Precalculus.) Let x now change by an amount Δx. Then the new x-coördinate is x + Δx.
It is the x-coördinate of Q on the graph.

But when the value of x changes, there is a resulting change Δy
in the value of y, that is, in the value of f(x). Its new value is f(x + Δx). The coördinates of Q are (x + Δx , f(x + Δx)).

Then

The derivative

Here, then, is the definition of the slope of the tangent line at P:

The slope of the tangent line at P
is the limit of the change in the function (the numerator)
divided by the change in the independent variable
as that change approaches 0.

Since Δx -- not x -- is the variable that approaches 0, x remains constant, and that limit will be a function of x. Since it will be derived from f(x), we call it the derived function or the derivative of f(x). To remind us that it was derived from f(x), we denote it by f '(x) -- "f-prime of x."

This quotient --

-- is called the Newton quotient, or the difference quotient. Calculating and simplifying it is a fundamental task in differential calculus.

Again, the difference quotient is a function of Δx. But to simplify the written calculations, then instead of writing Δx, we will write h.

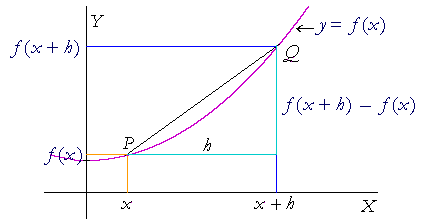
The derivative

Δx	=	h

Δy	=	f (x + h) − f (x)

The difference quotient then becomes:

We now express the definition of the derivative as follows.

DEFINITION 5. By the derivative of a function f(x), we mean the following limit, if it exists:

We call that limit the function f '(x) -- "f-prime of x" -- and when that limit exists, we say that f itself is differentiable at x, and that f has a derivative.

And so we take the limit of the difference quotient as h approaches 0. When that limit exists, that means that the difference quotient can be made as close to that limit -- "f '(x)" -- as we please. (Lesson 2.)

As for x, we are to regard it as fixed. It is the specific value at which we are evaluating f '(x).

In practice, we have to simplify the difference quotient before letting h approach 0. We have to express the numerator --

f (x + h) − f (x)

-- in such a way that we can divide it by h.

To sum up: The derivative is a function -- a rule -- that assigns to each value of x the slope of the tangent line at the point (x, f(x)) on the graph of f(x). It is the rate of change of f(x) at that point.

As an example, we will apply the definition to prove that the slope of the tangent to the function f(x) = x², at the point (x, x²), is 2x.

THEOREM.	f(x)	=	x²

implies

	f '(x)	=	2x.

Proof. Here is the difference quotient, which we will proceed to simplify:

1)		(x + h)² − x² h

2)	=	x² + 2xh + h² − x² h

3)	=	2xh + h² h

4)	=	2x + h.

In going from line 1) to line 2), we squared the binomial x + h. (Lesson 18 of Algebra.)

In going to line 3), we subtracted the x²s. That is, we subtracted f(x).

In going to line 4), we divided the numerator by h. (Lesson 20 of Algebra.)

We can do that because h is never equal to 0, even when we take the limit (Lesson 2).

We now complete the definition of the derivative and take the limit:

f '(x)	=		(2x + h)

	=	2x.

This is what we wanted to prove.

Whenever we apply the definition, we have to algebraically manipulate the difference quotient so that we can simply replace h with 0. In fact, the entire theory of limits, with all its complexities and subtleties, was invented to justify just that. (Poor Newton and Leibniz were criticized for offering justifications that the 19th century inventors of limits didn't like.) We may put h = 0 here because the difference quotient reduces to 2x + h, and is therefore a polynomial in h.

Problem. Let f(x) = x², and calculate the slope of the tangent to the graph --

a) at x = 5.

b) at x = −3. −6.

c) at x = 0. 0.

Differentiable at x

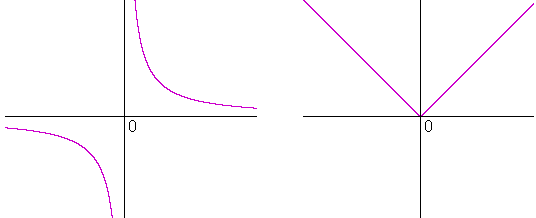
According to the definition, a function will be differentiable at x if a certain limit exists there. Graphically, this means that the graph at that value of x will have a tangent line. At which values, then, would a function not be differentiable?

Where it does not have a tangent line

Above are two examples. The function on the left does not have a derivative at x = 0, because the function is discontinuous there. At x = 0 there is obviously no tangent.

As for the graph on the right, it is the absolute value function, y = |x|. (Topic 5 of Precalculus.) And it is not possible to define the tangent line at x = 0, because the graph makes an acute angle there. In fact, the slope of the tangent line as x approaches 0 from the left, is −1. The slope approaching from the right, however, is +1. The slope of the tangent line at 0 -- which would be the derivative at x = 0 -- therefore does not exist . (Definition 2.2.)

The absolute value function nevertheless is continuous at x = 0. For, the left-hand limit of the function itself as x approaches 0 is equal to the right-hand limit, namely 0. This illustrates that continuity at a point is no guarantee of differentiability -- the existence of a tangent -- at that point.

(Conversely, though, if a function is differentiable at a point -- if there is a tangent -- it will also be continuous there. The graph will be smooth and have no break.)

Since differential calculus is the study of derivatives, it is fundamentally concerned with functions that are differentiable at all values of their domains. Such functions are called differentiable functions.

Can you name an elementary class of differentiable functions?

To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Think about this yourself first!

Polynomials.

Notations for the derivative

Since the derivative is this limit: then the symbol for the limit itself is (Read: "dee-y, dee-x.")

For example, if

y	=	x²,

then, as we have seen,
	=	2x.

"Dee-y, dee-x -- the derivative of y with respect to x -- is 2x."

We also write

y '(x) = 2x.

"y-prime of x is equal to 2x."

This symbol by itself:

d
dx

("dee, dee-x")

, is called the

differentiating operator. We are to take the derivative of what follows it.

For example,

d
dx

f(x) signifies the derivative with respect to x of f(x).

d dt	(4t³ − 5) signifies the derivative with respect to t
	of (4t³ − 5).

And so on.

A simple difference quotient

The difference quotient is a version of . And at times we will use the latter. That is, the change in the value of a function y = f(x) is y + Δy. Hence the difference quotient is

At times it will be convenient to express the difference quotient as

Note: As Δx approaches 0 -- as the point Q moves closer to P along the curve -- then Δy, or equivalently, Δf also approaches 0. That is,

The student should now do Problems that require the definition of the derivative.

Table of Contents | Home

Please make a donation to keep TheMathPage online.
Even $1 will help.

Questions or comments?

E-mail: teacher@themathpage.com