The derivative. Lesson 5, Section 2: Problems
The derivative of f(x) = 2x − 5
The equation of a tangent to a curve
Problem 1. Let f(x) = 2x − 5.
a) Write the difference quotient and simplify it.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| f(x + h) − f(x) h |
= | 2(x + h) − 5 − (2x − 5) h |
| = | 2x + 2h − 5 − 2x + 5 h |
|
| = | 2h h |
|
| = | 2. | |
b) Evaluate f '(x) at x = 9 and at x = −9.
| f '(x) | = | 2 | |
| = | 2, | ||
according to Theorem 4 of Lesson 2.
The rate of change of f(x) is 2 for all values of x. f '(x) is constant. But that should be obvious. y = 2x − 5 is the equation of a straight line whose slope is 2. (Topic 9 of Precalculus.) And the value of the slope of a straight line is the rate of change of y with respect to x -- so many units of y for each unit of x.
There is no tangent to a straight line, because a tangent, by definition, touches a curve at one point only.
Example. The equation of a tangent to a curve.
a) Calculate the slope of the line that is tangent to y = x2 at the point
a) on the curve where x = 4.
b) What is the equation of that line?
Solution.
a) The slope of the tangent to the curve at x = 4 is the value of the
a) derivative at x = 4. The derivative of y = x2 is 2x. Therefore at
a) x = 4, the slope of the tangent is 8.
b) The equation of a straight line has this form:
y = ax + b,
where a is the slope of the line. Therefore, since a = 8, the equation is
y = 8x + b.
To find the value of b, we can now proceed as in Solution 1 to Problem 1 in Lesson 34 of Algebra. Since x = 4 in the function y = x2, then y = 16. The coördinate pair (4, 16) will solve that equation:
| 16 | = | 8· 4 + b |
| = | 32 + b. | |
| Therefore, | ||
| b | = | −16. |
The equation of the tangent line is
y = 8x − 16.
See Problem 2f) below.
Problem 2 .
a) Calculate the derivative of f(x) = x3. Follow the sequence of
a) Problem 1.
a) [Hint: (a + b)3 = a3+ 3a2b + 3ab2 + b3. Topic 25 of Precalculus.]
| f(x + h) − f(x) h |
= | (x + h)3 − x3 h |
|
| = | x3 + 3x2h + 3xh2 + h3 − x3 h |
||
| = | 3x2h + 3xh2 + h3 h |
||
| = | 3x2 + 3xh + h2. | ||
| f '(x) | = | (3x2 + 3xh + h2) | |
| = | 3x2. | ||
b) Evaluate the slope of the tangent to y = x3 at x = 4.
The slope at x is 3x2. Therefore, at x = 4, the slope is 3· 16 = 48.
c) Evaluate the slope of the tangent to y = x3 at x = −2.
3· (−2)2 = 3· 4 = 12.
d) What is the rate of change of f(x) = x3 at x = −1.
3· (−1)2 = 3· 1 = 3.
At x = −1, the function is increasing at the rate of 3 units of y per unit of x.
e) What is the rate of change of that function at x = 5.
3· 52 = 3· 25 = 75.
At x = 5, the function is increasing at the rate of 75 units of y per unit of x.
f) What is the equation of the tangent to y = x3 at x = 5.
At x = 5, the slope of the tangent is 75. Therefore the equation of the tangent will be
y = 75x + b.
To find b, proceed as in the Example above.
When x = 5, then y = x3 = 125, so that the pair (5, 125) solve that equation.
125 = 75· 5 + b.
Therefore, b = −250. The equation of the tangent is
y = 75x − 250.
Problem 3. Prove: The straight line that is tangent to y = x2 at the point (a, a2), bisects the distance of a from the origin.
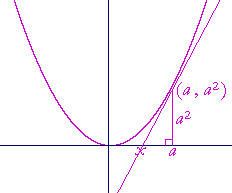
Let x be the x-intercept of the tangent line. Then we are to prove that x = a/2.
The vertical leg of that right triangle is a2. The horizontal leg is a − x. Therefore the slope of that line is
| a2 a − x |
. |
But the slope of that line is 2a because the derivative of x2 is 2x. Therefore,
| a2 a − x |
= | 2a |
| a2 | = | 2a(a − x) |
| a | = | 2(a − x) = 2a − 2x |
| 2x | = | 2a − a = a |
| x | = | a 2 |
Problem 4.
| a) Show: | d dx |
1 x |
= − | 1 x2 |
. |
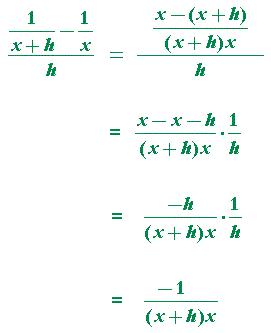
| d dx |
1 x |
= | ||
| = | ||||
To see how the difference quotient was simplified, see Lesson 3 of Precalculus, Problem 11c.
b) What is the rate of change of the function at x = 4?
| At x = 4, − |
1 x2 |
= − |
1 16 |
. The function is decreasing at the rate |
| of |
1 16 |
of a unit of y per unit of x. |
c) What is the rate of change of the function at x = ¼?
| At x = ¼, − |
1 x2 |
= −16. The function is decreasing at the |
rate of 16 units of y per unit of x.
Look at the graph. The closer to 0, the greater the rate of change. The further away from 0, the smaller the rate of change.
At every point of that graph, the tangent has a negative slope -- the derivative is always negative. As we move from left to right, the values of that function always decrease.
We have the following result, then:
| d dx |
1 x |
= − | 1 x2 |
. |
That is,
| d dx |
x−1 = −x−2. |
This has the form
| d dx |
xn = nxn −1 |
In what follows we will be exploiting that form.
![]()
Next Lesson: Rules for derivatives
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com