9
LINEAR FUNCTIONS
The Equation of a Straight Line
WE NOW BEGIN THE STUDY OF THE GRAPHS of polynomial functions.
We will find that the graph of each degree leaves its characteristic signature on the x- y-plane.
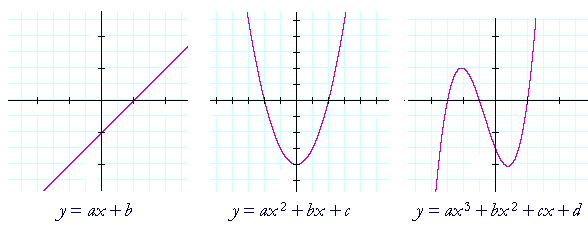
The graph of a first degree polynomial is always a straight line. The graph of a second degree polynomial is a curve known as a parabola. A polynomial of the third degree has the form shown on the right. Skill in coördinate geometry consists in recognizing this relationship between equations and their graphs. Hence the student should know that the graph of any first degree polynomial y =ax + b is a straight line, and, conversely, any straight line has for its equation, y =ax + b.
Sketching the graph of a first degree equation should be a basic skill. See Lesson 33 of Algebra.
Example. Mark the x- and y-intercepts, and sketch the graph of
y = 2x + 6.
Solution.
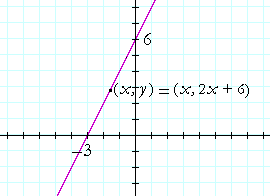
The x-intercept is the root. It is the solution to 2x + 6 = 0. The
x-intercept is −3.
The y-intercept is the constant term, 6.
Now, what does it mean to say that y = 2x + 6 is the "equation" of that line?
It means that every coördinate pair (x, y) that is on the graph, solves that equation. (That's what it means for a coördinate pair to be on the graph on any equation.) Every coördinate pair (x, y) on that line is
(x, 2x + 6).
That line, therefore, is called the graph of the equation y = 2x + 6. And y = 2x + 6 is called the equation of that line.
Every first degree equation has for its graph a straight line. (We will prove that below.) For that reason, functions or equations of the first degree -- where 1 is the highest exponent -- are called linear functions or linear equations.
Problem 1. Mark the x- and y-intercepts, and sketch the graph of
y = −3x − 3
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
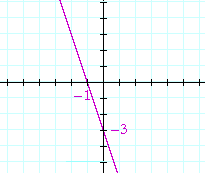
The x-intercept is the solution to −3x − 3 = 0. It is x = −1. The y-intercept is the constant term, −3.
Problem 2. Sketch the graph of y = −4.
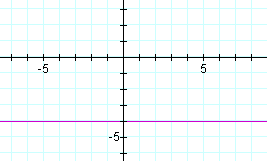
An equation of the form y = A number, is a horizontal line.
See Lesson 33 of Algebra, the section "Vertical and horizontal lines."
The slope-intercept form
This linear form
y = ax + b
is called the slope-intercept form of the equation of a straight line. Because, as we shall prove presently, a is the slope of the line (Topic 8), and b -- the constant term -- is the y-intercept.
This first degree form
Ax + By + C = 0
where A, B, C are integers, is called the general form of the equation of a straight line.
Theorem. The equation
y = ax + b
is the equation of a straight line with slope a and y-intercept b.
For, a straight line may be specified by giving its slope and the coördinates of one point on it. (Theorem 8.3.)
Therefore, let the slope of a line be a, and let the one point on it be its y-intercept, (0, b).
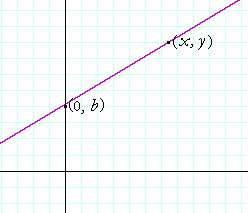
Then if (x, y) are the coördinates of any point on that line, its slope is
| y − b x − 0 |
= | y − b x |
= a. |
On solving for y,
y = ax + b.
Therefore, since the variables x and y are the coördinates of any point on that line, that equation is the equation of a straight line with slope a and y-intercept b. Which is what we wanted to prove.
The slope of a straight line -- that number -- indicates the rate at which the value of y changes with respect to the value of x. (Topic 8.)
Problem 3. Name the slope of each line, and state the meaning of each slope.
a) y = 2x + 6
The slope is 2. This means that y increases 2 units for every 1 unit of x.
| b) y = − | 2 3 |
x + 4 |
| The slope is − | 2 3 |
. This means that y decreases 2 units for every |
| 3 units of x. | ||
c) y = x
The slope is 1. This means that y increases 1 unit for every 1 unit of x. This is the identity function.
See Lesson 5.
d) 3x + 3y = 1
It is only when y = ax + b, that the slope is a. Therefore, on solving for y: y = −x + 1/3. The slope is −1. This means that y decreases 1 unit for every unit that x increases.
Next Topic: Quadratics: Polynomials of the 2nd degree
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
