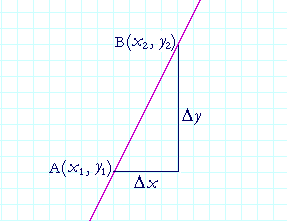8
THE SLOPE
OF A STRAIGHT LINE
The specification of a straight line
IN LESSON 33 OF ALGEBRA we discuss the equation of a straight line. Sketching the graph of the equation of a line should be a basic skill.
Consider this straight line.
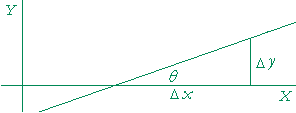
The (x, y) coördinates at B have changed from the coördinates at A. By the symbol Δx ("delta x") we mean the change in the x-coördinate. That is,
Δx = x2 − x1.
Similarly, Δy ("delta y") signifies the resulting change in the y-coördinate.
Δy = y2 − y1.
Δx is the horizontal leg of that right triangle; Δy is the vertical leg.
By the slope of a straight line, then, we mean this number:
| Slope | = | _Vertical leg_ Horizontal leg |
= | Δy Δx |
= |
For example,
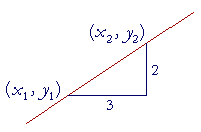
If the value of y changes by 2 units when the value of x changes by 3, then the slope of that line is the number
![]() .
.
What does slope ![]() mean? It indicates the rate at which a change in the value of x produces a change in the value of y. 2 units of y per -- for every -- 3 units of x.
mean? It indicates the rate at which a change in the value of x produces a change in the value of y. 2 units of y per -- for every -- 3 units of x.
For every 3 units that line moves to the right, it will move up 2. That will be true between any two points on that line. Over 6 and up 4, over 15 and up 10. A straight line has one and only one slope. (Theorem 8.1 below.)
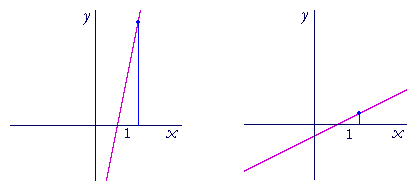
In each of those lines, the x-coördinate has increased by 1 unit. In the line on the left, however, the corresponding value of y has increased much more than in the line on the right. The line on the left has a greater slope than the line on the right. The value of y has changed at a much greater rate.
The tangent to a curve
In calculus, the student will see that the slope of a tangent line to a curve at a point P --
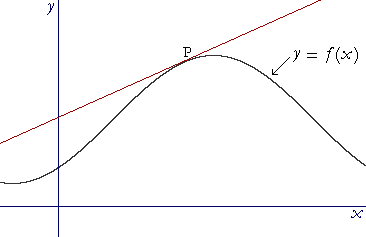
-- is the geometrical meaning of what is called the derivative. It indicates the typically non-constant rate of change of y with respect to x -- at the point of tangency.
The slope of a straight line is very definitely a topic of precalculus.
In a typical application, the x-axis represents time and the y-axis, distance. The rate of change of distance with respect to time -- the speed -- is typically not constant. The graph is not a straight line. The slope of the tangent line gives the instantaneous speed at a specific moment of time.
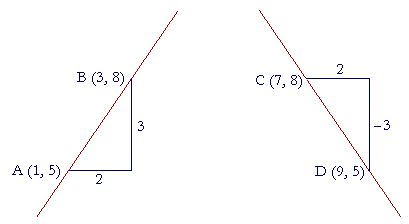
Which line do we say is sloping "up"? And which is sloping "down"?
Since we imagine moving along the x-axis from left to right, we say that the line on the left is sloping up, and the line on the right, down.
What is more, a line that slopes up has a positive slope. While a line that slopes down has a negative slope.
For, both the x- and y-coördinates of B are greater than the coördinates of A, so that both Δx and Δy are positive. Therefore their quotient, which is the slope, is positive.
But while the x-coördinate of D is greater than the x-coördinate of C, so that Δx is positive, the y-coördinate of D is less than the y-coördinate of C, so that Δy, 5 − 8, is negative. Therefore that quotient is negative.
Problem 1. What number is the slope of each line?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | 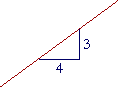 |
b) | 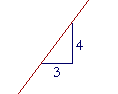 |
|||||
| 3 4 |
4 3 |
|||||||
| c) | 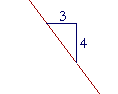 |
d) | 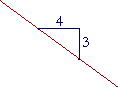 |
|||||||
| − | 4 3 |
− | 3 4 |
|||||||
Horizontal and vertical lines
What number is the slope of a horizontal line -- that is, a line parallel to the x-axis? And what is the slope of a vertical line?
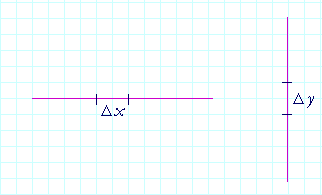
A horizontal line has slope 0 because even though the value of x changes, the value of y does not. Δy = 0.
| Δy Δx |
= | 0 Δx |
= | 0. | (Lesson 5) |
For a vertical line, however, the slope is not defined. The slope tells how the y-coördinate changes when the x-coördinate changes. But the x-coördinate does not change -- Δx = 0. A vertical line does not have a slope.
| Δy Δx |
= | Δy 0 |
= | No value. | (Lesson 5) |
Problem 2.
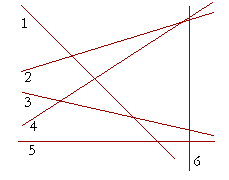
a) Which numbered lines have a positive slope? 2 and 4.
b) Which numbered lines have a negative slope? 1 and 3.
c) What slope has the horizontal line 5? 0.
c) What slope has the vertical line 6? It does not have a slope.
Problem 3. Calculate the slope of the straight line joining the points (−1, −2) and (7, −8). And what does that slope mean?
| Δy Δx |
= | −8 − (−2) 7 − (−1) |
= | −8 + 2 7 + 1 |
= | −6 8 |
= − | 3 4 |
That slope indicates the rate of change of the y-coördinate with respect to the x-coördinate. For every 4 units the x-coördinate increases, the y-coördinate decreases by 3.
Problem 4. Let y = f(x) = x2 − 1, and let two points on its graph have these x-coördinates: x1 = 3, x2 = 5. Calculate the slope of the straight line that passes through those two points.
At each of those points, f(x) will give the value of y. At x1 = 3, y1 = 32 − 1 = 8. At x2 = 5, y2= 52 − 1 = 24. Therefore the two points are (3, 8) and (5, 24). And therefore, Δy/Δx =
(24 − 8)/(5 − 3) = 16/2 = 8.
Problem 5.
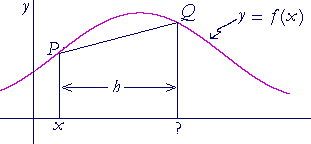
Let y = f(x), and let its graph pass through two points P and Q whose x-coördinates are separated by a distance h. And let x be the x-coördinate of P.
a) What is the x-coördinate of Q? x + h
b) What are the x- and y-coördinates of P? (x, f(x))
c) What are the coördinates of Q? (x + h, f(x + h))
d) Write an expression for the slope of the straight line joining the
d) points P and Q.
| f(x + h) − f(x) h |
This is the famous difference quotient of calculus. (Topic 3.) The question calculus asks is: What is the value of that slope when h is practically 0? The answer will be the slope of the tangent line at P. That slope will be the rate of change of the function at P.
See Topic 3, Problem 11.
One slope
To establish the algebraic equation of any geometrical figure, we must carry over our knowledge from plane geometry; for nothing will come of nothing. With the aid of the following theorems, we will be able to prove that the equation of a straight line may take the form y = ax + b, and that a is the slope of the line. We will do that in the following Topic.
First,
Theorem 8.1. A straight line has one slope.
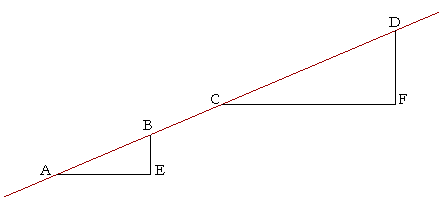
That is, whether we measure the slope by moving from point A to point B, or by moving from point C to point D, the number we obtain will be the same.
For, if we measure the slope from A to B, we will get BE/EA. While if we measure it between C and D, we will get DF/FC.
But FC is parallel to EA because they are both parallel to the x-axis;
and DA is a straight line that falls on two parallel straight lines;
therefore, the exterior angle DCF is equal to the opposite interior angle on the same side, angle BAE. (Euclid, I. 29)
Therefore the right triangles BEA, DFC are similar (Euclid, VI. 4), and therefore, proportionally,
| BE EA |
= | DF FC |
. |
| Δy Δx |
will be the same, whether we go from A to B, or from C to D. |
That is what we wanted to prove.
Problem 6. A straight line will make an angle θ with the x-axis.
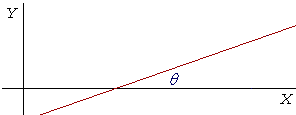
Which trigonometric function of θ is its slope?
tan θ. For, a line has one slope.
"Same slope" and "parallel"
Before we state the next theorem, the student should be familiar with the logical expression if and only if.
First, if p and q are statements (sentences), then in the proposition "If p, then q," p is called the hypothesis. It is what we are given, or what we assume. There is no logic without hypotheses.
Statement q is called the conclusion. It is what we must prove on the basis of the hypothesis.
The proposition "If q, then p" is called the converse of "If p, then q." The hypothesis and conclusion are exchanged.
Finally, the proposition "p if and only if q" means: "If p, then q , and if q, then p." In other words, a proposition and its converse are both true.
For example, "A triangles is isosceles if and only if the base angles are equal." This means, "If a triangle is isosceles, then the bases angles are equal; and, conversely, if the base angles are equal, then the triangle is isosceles."
Therefore, when we prove an if and only if proposition, we must prove both a proposition and its converse.
*
The slope of a line is a number. Parallel is a geometrical property. The relationship between them is the next theorem.
Theorem 8.2. Two straight lines are parallel if and only if they have the same slope.
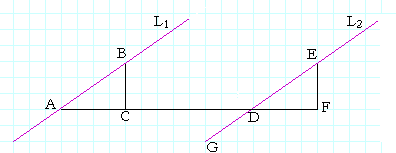
Let the straight lines L1, L2 be parallel. And let the slope of L1 be BC/CA; for a straight line has only one slope. (Theorem 1)
Draw the straight line ACF intersecting L2 at D, and draw FE perpendicular to DF.
Then the slope of the straight line L2 is EF/FD.
Then the slope of L2 is equal to the slope of L1. That is,
| BC CA |
= | EF FD |
For, since the lines L1, L2 are parallel, and the straight line AF falls on them, the alternate angles BAC, EDF are equal (Euclid, I. 29);
therefore the right triangles BAC, EDF are similar (Euclid, VI.4),
and those sides are proportional that contain the equal angles:
| BC CA |
= | EF FD |
Therefore the straight lines L1, L2 have the same slope.
Next, conversely, assume that those lines have the same slope:
| BC CA |
= | EF FD |

Then the two straight lines are parallel.
For, the angles at C and F are right angles and therefore equal,
and by assumption, the sides that make them are proportional.
But if two triangles have one angle equal to one angle, and the sides that make them are proportional, then the triangles are similar,
and those angles are equal that are opposite the corresponding sides;
(Euclid, VI. 6, 4)
therefore, angle BAC is equal to angle EDF.
But angle CDG is equal to angle EDF because they are vertical angles;
(Euclid, I. 15)
therefore angle BAC is equal to angle CDG.
That is, the straight line AF falling on the straight lines L1, L2 makes the alternate angles BAC, CDG equal.
Therefore the straight line L1is parallel to the straight line L2.
(Euclid, I. 27)
Therefore two straight lines are parallel if and only if they have the same slope. Which is what we wanted to prove.
As for perpendicular lines, in Lesson 34 of Algebra we prove the following:
If two straight lines are perpendicular to one another, then the product of their slopes is −1.
That is, if the slope of one line is m, then the slope of the perpendicular line
| is − | 1 m |
. |
The specification of a straight line
Finally, we can state
Theorem 8.3. A straight line may be specified by giving its slope and the coördinates of one point on it. Equivalently: Through any point there is exactly one straight line with a given slope.
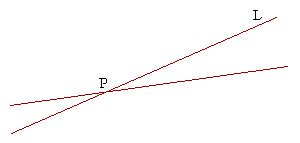
Let the straight line L have slope m, and let it pass through the point P. Then L is the only straight line through P with slope m.
For, it will be impossible to draw another straight line through P parallel to L, because parallel lines do not meet.
Therefore, any two lines through P will not be parallel, and therefore they will have different slopes. (Theorem 2)
Therefore, there is only one straight line through P with a given slope.
This means that a straight line may be specified by giving its slope and the coördinates of one point on it.
Which is what we wanted to prove.
*
On the basis of this theorem, we will be able to prove, in the following Topic, that the equation of a line may take the form y = ax + b, where a is the slope of the line, and b is the y-intercept.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com