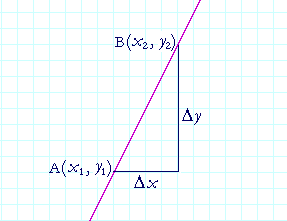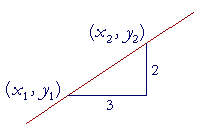34
THE SLOPE OF A
STRAIGHT LINE
Parallel and perpendicular lines
IN THE PREVIOUS LESSON, we took up the equation of a straight line. Sketching the graph of the equation of a line is a basic skill.
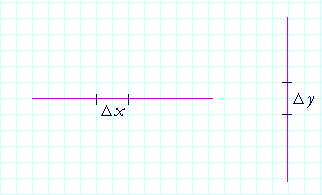
Consider this straight line. The (x, y) coördinates at B have changed from the coördinates at A. By the symbol Δx ("delta x") we mean the change in the x-coördinate. That is,
Δx = x2 − x1.
(As for using the subscripts 1 and 2, see Lesson 32, the section, The distance bewteen any two points.)
Similarly, Δy ("delta y") signifies the resulting change in the y-coördinates.
Δy = y2 − y1.
Δx is the horizontal leg of that right triangle; Δy is the vertical leg.
By the slope of a straight line, then, we mean this number:
| Slope | = | _Vertical leg_ Horizontal leg |
= | Δy Δx |
= |  |
For example,
If the value of y changes by 2 units when the value of x changes by 3, then the slope of that line is 
.
What does slope mean? It indicates the rate at which a change in the value of x produces a change in the value of y. 2 units of y per -- for every -- 3 units of x.
For every 3 units that line moves to the right, it will move up 2. That will be true between any two points on that line. Over 6 and up 4, over 15 and up 10. Because a straight line has one and only one slope. (Theorem 8.1 of Precalculus.)
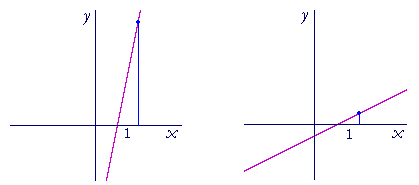
In each line above, the x-coördinate has increased by 1 unit. In the line on the left, however, the value of y has increased much more than in the line on the right. The line on the left has a greater slope than the line on the right. The value of y has changed at a much greater rate.
If the x-axis represents time and the y-axis distance, as is the case in many applications, then the rate of change of y with respect to x -- of distance with respect to time -- is called speed or velocity. So many miles per hour, or meters per second.
Up or down?
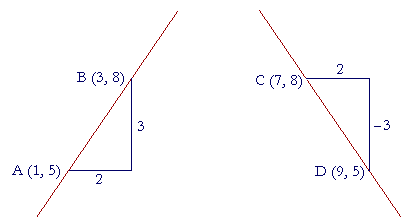
Which line do we say is sloping "up"? And which is sloping "down"?
Since we imagine moving along the x-axis from left to right, we say that the line on the left is sloping up, and the line on the right, down.
What is more, when a line slopes up, the slope is a positive number. When a line slopes down, it is a negative number.
For, both the x- and y-coördinates of B are greater than the coördinates of A, so that both Δx and Δy are positive. Therefore their quotient, which is the slope, is positive.
But while the x-coördinate of D is greater than the x-coördinate of C, so that Δx is positive, the y-coördinate of D is less than the y-coördinate of C. Δy, 5 − 8, is negative. Therefore that quotient is negative.
Example 1. What number is the slope of each line?
a)
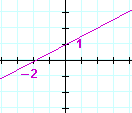
You should see immediately that this is a line of positive slope. Do not be fooled by the xx-coördinate −2. Δx is still positive. In fact, you should always consider Δx to be positive. Let Δy determine the sign.
The slope of this line is ½.
b)
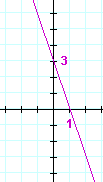
You should see that this is a line of negative slope. Its value is −3.
Problem 1. What number is the slope of each line?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) |  |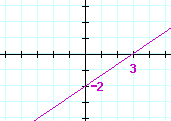
b) |  |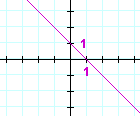
|||||
| 2 3 |
−1 | |||||||
| c) |  |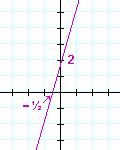
d) |  |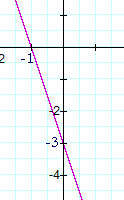
|||||||
| 4 | −3 | |||||||||
Horizontal and vertical lines
What number is the slope of a horizontal line -- that is, a line parallel to the x-axis? And what is the slope of a vertical line?
A horizontal line has slope 0, because even though the value of x changes, the value of y does not. Δy = 0.
| Δy Δx |
= | 0 Δx |
= | 0. | (Lesson 6) |
A vertical line, however, does not have a slope. The slope tells how the y-coördinate changes when the x-coördinate changes. But the x-coördinate does not change. Δx = 0.
| Δy Δx |
= | Δy 0 |
= | No value. | (Lesson 6) |
Problem 2.
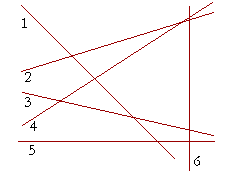
a) Which numbered lines have a positive slope? 2 and 4.
b) Which numbered lines have a negative slope? 1 and 3.
c) What slope has the horizontal line 5? 0.
d) What slope has the vertical line 6? It does not have a slope.
Example 2. Calculate the slope of the line that passes through the points (3, 6) and (1, 2).
Solution. To do this problem, here again is the definition of the slope. It is this number:
| Δy Δx |
= |  |
Therefore, the slope of the line passing through (3, 6) and (1, 2) is:
| Δy Δx |
= | 6 − 2 3 − 1 |
= | 4 2 |
= | 2 1 |
= 2. |
Note: It does not matter which point we call the first and which the second. But if we calculate Δy starting with (3, 6), then we must calculate Δx also starting with (3, 6).
As for the meaning of slope 2: On the straight line that joins those two points, the value of y will change by 2 units for every 1 unit the value of x changes. That is the rate of change of y with respect to x. 2 for every 1.
Problem 3. Calculate the slope of the line that joins these points.
| a) | (1, 5) and (4, 17) | b) | (−3, 11) and (−5, 15) | |||||||||
| 17 − 5 4 − 1 |
= | 12 3 |
= | 4 | _ 15 − 11 _ −5 − (−3) |
= | 4 −2 |
= | −2. | |||
| c) | (1, −1) and (−7, −5) | d) | (2, −9) and (−2, −5) | |||||||||
| −5 − (−1) −7 − 1 |
= | −4 −8 |
= | ½ | −9 − (−5) 2 − (−2) |
= | −4 4 |
= | −1 | |||
The slope-intercept form
This linear form
y = ax + b
is called the slope-intercept form of the equation of a straight line. Because, as we can prove (Topic 9 of Precalculus): a is the slope of the line and b is the y-intercept.
Problem 4. What number is the slope of each line, and what is the meaning of each slope?
a) y = 5x − 2
The slope is 5. This means that y increases 5 units for every 1 unit x increases. That is the rate of change of y with respect to x.
| b) y = − | 2 3 |
x + 4 |
| The slope is − | 2 3 |
. |
This means that y decreases 2 units for every 3 units of x..
Problem 5.
| a) | Write the equation of the line whose slope is 3 and whose y-intercept is 1. |
y = 3x + 1
| b) | Write the equation of the line whose slope is −1 and whose y-intercept is −2. |
y = −x − 2
| c) | Write the equation of the line whose slope is and which passes through the origin. |
| y = | 2 3 |
x. The y-intercept b is 0. |
Problem 6. In Problem 1, write the equation of each line.
| a) y = | 2 3 |
x − 2. | b) y = −x + 1. | |
| c) y = 4x + 2. | d) y = −3x − 3. | |||
The general form
This linear form
Ax + By + C = 0
where A, B, C are integers, is called the general form of the equation of a straight line.
Problem 7. What number is the slope of each line, and what is its meaning?
a) x + y − 5 = 0
This line is in the general form. It is only when the line is in the slope-intercept form, y = ax + b, that the slope is a. Therefore, on solving for y: y = −x + 5. The slope therefore is −1. This means that the value of y decreases 1 unit for every unit that the value of x increases.
5, incidentally, is b, the y-intercept.
| b) | 2x − 3y + 6 | = | 0 | |||
| −3y | = | −2x − 6 | ||||
| y | = | 2 3 |
x + 2, | on dividing every term by −3. | ||
The slope therefore is . This means that the line goes up 2 units for every 3 it goes over.
| c) | Ax + By + C | = | 0 | |||||
| By | = | −Ax − C | ||||||
| y | = | − | A B |
x | − | C B |
, on dividing every term by B. | |
| The slope is − | A B |
. |
We can view that as a formula for the slope when the equation is in the general form. For example, if the equation is
4x − 5y + 2 = 0,
then the slope is
| − | 4 −5 |
= | 4 5 |
. |
Parallel and perpendicular lines
Straight lines will be parallel if they have the same slope. The following are equations of parallel lines:
y = 3x + 1 and y = 3x − 8.
They have the same slope 3.
Straight lines will be perpendicular if
| 1) | their slopes have opposite signs -- one positive and one negative, and | |
| 2) | they are reciprocals of one another. | |
That is:
If m is the slope of one line, then a perpendicular line has slope −
.
To be specific, if a line has slope 4, then every line that is perpendicular to it has slope −¼.
(We will prove that below.)
Problem 8. Which of these lines are parallel and which are perpendicular?
| a) y = 2x + 3 | b) y = −2x + 3 | c) y = ½x + 3 | d) y = 2x − 3 |
a) and d) are parallel. b) and c) are perpendicular.
Problem 9. If a line has slope 5, then what is the slope of a line that is perpendicular to it? 
Problem 10. If a line has slope − , then what is the slope of a perpendicular line? 
Problem 11. If a line has equation y = 6x − 5, then what is the slope of a perpendicular line? 
Theorem: The slopes of perpendicular lines
If two straight lines are perpendicular to one another, then the product of their slopes is −1.
That is: If the slope of one line is m, then the slope of the perpendicular
| line is − | 1 m |
. |
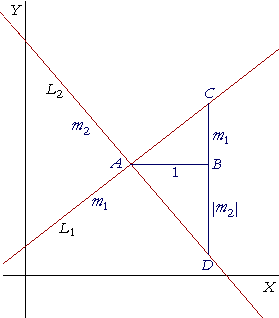
Let L1 be a straight line, and let the perpendicular straight line L2 cross L1 at the point A.
Let L1 have slope m1, and let L2 have slope m2. Assume that m1 is positive. Then m2, as we will see, must be negative.
Draw a straight line AB of length 1 parallel to the x-axis, and draw BC at right angles to AB equal in length to m1.
Extend CB in a straight line to join L2 at D.
Now, since the straight line L2 has one slope m2 (Theorem 8.1 of Precalculus), the length of BD will be |m2|. For in going from A to D on L2, we go over 1 and down |m2|.
That is, m2 is a negative number.
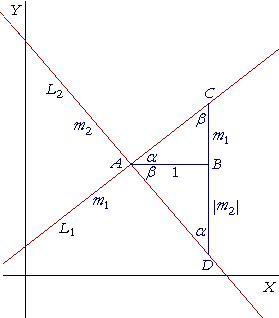
(Same figure.)
Angle CAD is a right angle. Therefore angle a is the complement of angle ß.
But triangle ABD is right-angled, and therefore the angle at D is also the complement of angle ß;
therefore the angle at D is equal to angle a.
The right triangles ABC, ABD therefore are similar (Topic 5 of Trigonometry),
and the sides opposite the equal angles are proportional:
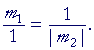
This implies
m1m2| = 1.
But m2 is negative. Therefore,
m1m2 = −1.
Which is what we wanted to prove.
Next Lesson: Simultaneous linear equations
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com